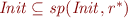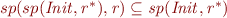Space of Invariants
Problem Statement
Let  be a set (e.g. the set of all integers). Let
be a set (e.g. the set of all integers). Let  and
and 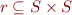 . Define
. Define
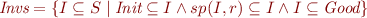
For each element 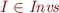 we have
we have 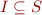 and we think of
and we think of  as an invariant.
as an invariant.
Prove each of the following statements or give a counterexample.
a): If 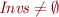 , then
, then 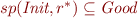 .
.
b): The set  is finite.
is finite.
c): If  then also
then also  .
.
d): If  then also
then also  .
.
e): Let  and let
and let

in other words, by definition of  ,
,
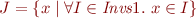
Prove that then 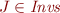 . What do we obtain for
. What do we obtain for 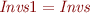 ?
?
f): Let  and let
and let
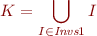
in other words, by definition of  ,
,
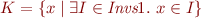
Prove that then 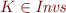 . What do we obtain for
. What do we obtain for 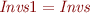 ?
?
g): Is the set 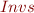 a lattice? If it is a lattice, is it complete? If it is not a lattice, can it be modified to become a
lattice?
a lattice? If it is a lattice, is it complete? If it is not a lattice, can it be modified to become a
lattice?
Solutions
Solution a)
True.
First we prove the following lemme using induction on  .
.
Lemma
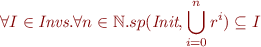
Base. Assume  .
.
We show 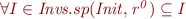 .
.
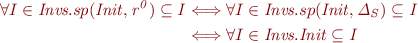
This holds according to the definition of invariants.
Inductive step. Assume  .
We show
.
We show  .
.
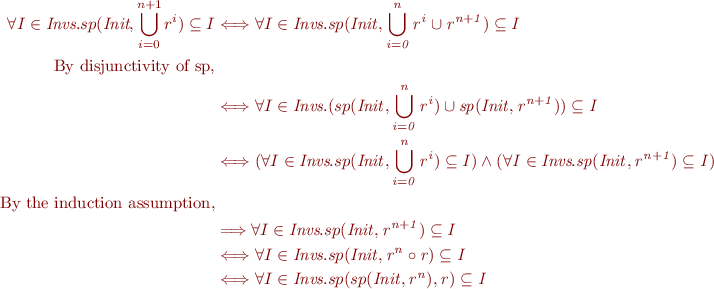
By the induction assumption we know  .
.
We can easily show for two invariants  and
and 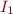 that
that 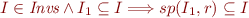 .
This proves the lemma.
.
This proves the lemma.
From the lemma we can conclude 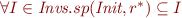 .
.
The set  is non-empty, so there exists
is non-empty, so there exists 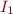 such that
such that 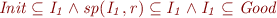 .
This shows that
.
This shows that 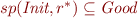 .
.
Solution b)
False.
You can easily find counter-examples.
Solution c,d)
Both true.
The assumption  gives us the following.
gives us the following.
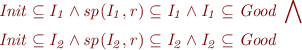
From the set theory we know that if  and
and 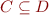 then we can conclude both
then we can conclude both
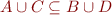 and
and 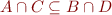 .
.
We can use this fact on the on the corresponding components:
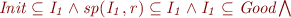
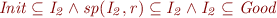
Computing the union gives us:
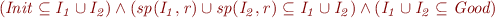
Due of the disjunctivity of 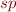 we can conclude that
we can conclude that  is an invariant.
is an invariant.
For the intersection case we replace the invariant of 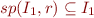 with a stronger one
with a stronger one 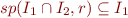 .
Similarly for
.
Similarly for 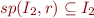 .
.
This can be done due to the monotonicity of 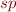 .
.
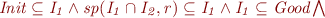

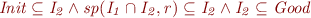
The proof is similar to the union case.
Solution e)
Consider the following equivalence.
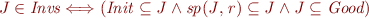
We show that each conjunct is valid.
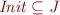 . Holds since
. Holds since  is included in every invariant.
is included in every invariant.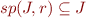
Let  be an arbitrary member of
be an arbitrary member of 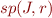 .
.
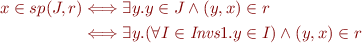
Nested quantifiers can be swapped, but the reverse does not necessarily hold.
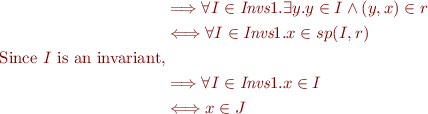
 . Holds if
. Holds if  is non-empty.
is non-empty.
If 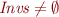 and
and 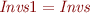 we claim
we claim 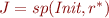 .
.
We proved in (a) that 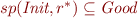 .
It remains to prove the other two conditions.
.
It remains to prove the other two conditions.
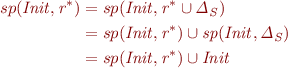
Which shows that  is included in
is included in 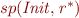 .
.
This is correct because 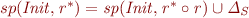
To prove that 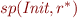 is the bottom element we have to prove the following.
is the bottom element we have to prove the following.
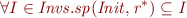
Which was proved in a lemma in part (a).
Solution f)
Consider the following equivalence.
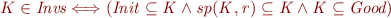
We show that each conjunct is valid.
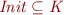 . Holds since
. Holds since  is included in every invariant.
is included in every invariant.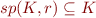
Let  be an arbitrary member of
be an arbitrary member of 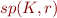 .
.
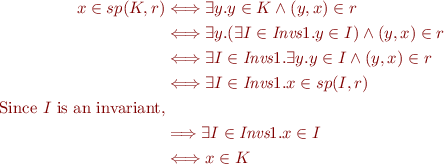
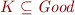 . Holds if
. Holds if  is non-empty.
is non-empty.
If 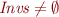 and
and 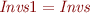 we claim
we claim 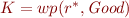 .
.
To prove that 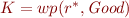 is the top element we have to prove the following.
is the top element we have to prove the following.
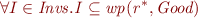
We prove the following lemme using induction on  .
.

Base. Assume  .
.
We show 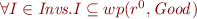 .
.
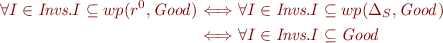
This holds according to the definition of invariants.
Inductive step. Assume  .
We show
.
We show  .
.
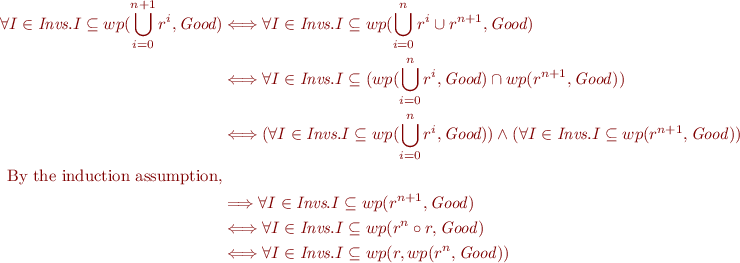
By the induction assumption we know  .
.
We can also easily show for two invariants  and
and  that
that 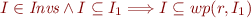 .
Note that the condition
.
Note that the condition 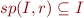 is equivalent to
is equivalent to 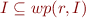 .
.
This proves the lemma.
Solution g)
The ordered set 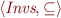 is a lattice.
We proved in part (c ) and (d) that for any
is a lattice.
We proved in part (c ) and (d) that for any  both
both  and
and  exist and
are equal to
exist and
are equal to  and
and  respectively.
respectively.
We showed in part (e) and (f) that for every subset 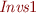 both lub and gub exist:
both lub and gub exist: 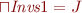 and
and 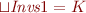 .
.
The lattice is complete.
The top element is 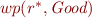 and the bottom element is
and the bottom element is 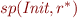 .
.