Homework 03: Solutions
Problem 1
Let  be the set of all first-order formulas (viewed as syntax trees, so e.g.
be the set of all first-order formulas (viewed as syntax trees, so e.g. 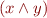 is a different formula from
is a different formula from 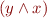 and let
and let  be the implication relation on formulas:
be the implication relation on formulas:
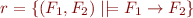
Check whether  is reflexive, antisymmetric, and transitive relation.
is reflexive, antisymmetric, and transitive relation.
Solution
The relation is both reflexive and transitive.
It is not antisymmetric. As a counterexample consider the example that is given in the problem statement: 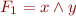 and
and 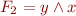
Problem 2
Let 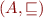 be a partial order such that every set
be a partial order such that every set  has the greatest lower bound. Prove that then every set
has the greatest lower bound. Prove that then every set  has the least upper bound.
has the least upper bound.
Problem 3
Galois connection is defined by two monotonic functions  and
and 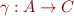 between partial orders
between partial orders  on
on  and
and  on
on  , such that
, such that

for all  and
and  (intuitively, the condition means that
(intuitively, the condition means that  is approximated by
is approximated by  ).
).
Part a) Show that the condition  is equivalent to the conjunction of these two conditions:
is equivalent to the conjunction of these two conditions:
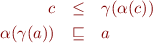
hold for all  and
and  .
.
Part b) Let  and
and  satisfy the condition of Galois connection. Show that the following three conditions are equivalent:
satisfy the condition of Galois connection. Show that the following three conditions are equivalent:
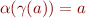 for all
for all 
 is a surjective function
is a surjective function is an injective function
is an injective function
Problem 4
Consider Problem 3 on the Space of Invariants in the previous homework, Homework 02.
a): Is the set 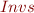 a lattice? If it is a lattice, is it complete? If it is not a lattice, can it be modified to become a lattice?
a lattice? If it is a lattice, is it complete? If it is not a lattice, can it be modified to become a lattice?
b): From now on, fix the relation  . Define
. Define 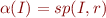 and define
and define 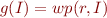 . Are functions
. Are functions  and
and  monotonic? Do they form a Galois connection? Prove or give a counterexample.
monotonic? Do they form a Galois connection? Prove or give a counterexample.
c): For each of the functions  ,
,  , describe the space of prefix points, postfix points, as well as the least and the greatest fixpoints. You may find Fixed Point Theorems useful.
, describe the space of prefix points, postfix points, as well as the least and the greatest fixpoints. You may find Fixed Point Theorems useful.