• If you think you may attend the class, send emails to {viktor.kuncak, ruzica.piskac, hossein.hojjat} saying that you plan to attend. Also, please register in the online system.
• - This part is in case you do not know Scala already. Its purpose is to give you the feeling how does pattern matching in Scala work. Make sure you have access to a working Scala language installation and learn how to use Pattern Matching in Scala. Some very simple examples that use pattern matching is this binary search in Scala:

sealed abstract class BST {
  def contains(key: Int): Boolean = (this : BST) match { 
    case Node(left: BST,value: Int, _) if key < value => left.contains(key)
    case Node(_,value: Int, right: BST) if key > value => right.contains(key)
    case Node(_,value: Int, _) if key == value => true
    case e : Empty => false
  }
}
case class Empty extends BST
case class Node(val left: BST, val value: Int, val right: BST) extends BST

object BinarySearchTree {
  def main(args: Array[String]): Unit =
    if (Node(Node(Empty(),3,Empty()),5,Empty()).contains(3)) println("Inside")
    else println("Outside")
}

You should be able to save this file as BinarySearchTree.scala, compile it with “scalac BinarySearchTree.scala”, run it with “scala BinarySearchTree”, and obtain as a result “Inside”.

Recall Proving Correctness of Some Small Examples from the class. Consider the following annotated procedure that computes multiplication of arguments, but iterates backwards:

private static int fi3(int x, int y)
/*: requires "x >= 0 & y >= 0"
    ensures "result = x * y" */
{	
  int r = 0;
  int i = y;
  while //: inv "..."
     (i > 0) {
    i = i - 1;
    r = r + x;
  }
  return r;
}

Write a loop invariant for this procedure that is sufficient to prove the postcondition result = x * y. Prove that the invariant satisfies all three conditions in the Notion of Inductive Loop Invariant.

The following is a skeleton of an iterative version to the recursive procedure in Proving Correctness of Some Small Examples.

private static int fip(int x, int y)
/*: requires "x >= 0 & y >= 0"
    ensures "result = x * y" */
{	
  int y1 = y;
  int a = x;
  int r = 0;
  while /*: inv "..." */
     (y1 > 0) {
    if (y1 % 2 != 0) {
      r = ...
      y1 = ...
    }
    y1 = ...
    a = ...
  }
  return r;
}

Complete the code with appropriate expressions, find the loop invariant, and prove that it satisfies all three conditions in the Notion of Inductive Loop Invariant.

Consider the definition of abstract syntax trees for propositional formulas in Scala, built from operators for negation, conjunction, disjunction, and implication.

Write the evaluation function that takes a mapping from variable names to truth values and returns the truth value of the formula.

You can find a skeleton that is a good starting point for this problem and the next one in file propositional.scala.txt (remove the “.txt” file name suffix after saving the file).

Negation-normal form of a propositional formula contains only conjunction, disjunction, and negation operators. Such formula should not contain implication operator. Moreover, negation only can only apply to variables and not to other formulas. The following tautologies can be used to transform formula to negation normal form:

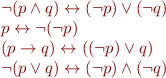
Extend the solution for the previous problem with a function that takes formula syntax tree and transforms it into an equivalent formula in negation-normal form. For example, the function should transform formula into formula .

Write also code that tests transformation to normal form by repeating several times the following steps:

• generate a random assignment to propositional variables of the formula
• compare the truth value of the original and of the transformed formula

Implement a DPLL Algorithm for SAT. You can also use various Advanced SAT solving Techniques. Your solver has to accept an input in DIMACS format. More about the DIMACS format you can find at: ftp://dimacs.rutgers.edu/pub/challenge/satisfiability/.