Forward Symbolic Execution
Can be used for
- verification condition generation
- executing programs
- testing, bug finding
- proving programs correct (if extended with techniques for loop invariants)
Intuition for Symbolic Execution
Symbolic execution engine is like an interpreter, but can keep values of variables symbolic, and keep track of constraints on these symbolic values. This is why it is called symbolic execution. In the special case when the input values are known (and there is no I/O in the program), it reduces to execution (interpretation).
State of Symbolic Execution Engine
Assume for simplicity:
- the set of variables is
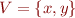
- there are no loops
Symbolic execution maintains a formula 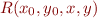 describing the relation between the initial state and the current state.
describing the relation between the initial state and the current state.
The engine ensures that 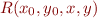 has the following normal form:
has the following normal form:
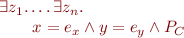
where
 is a term describing symbolic state of
is a term describing symbolic state of 
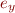 describes symbolic state of
describes symbolic state of 
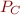 is a path condition
is a path condition- variables
 do not appear in
do not appear in 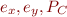 (they only appear on LHS of
(they only appear on LHS of 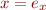 ,
,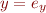 .
.  are fresh variables that do not appear in the program (we often omit existential quantification over these variables)
are fresh variables that do not appear in the program (we often omit existential quantification over these variables)
Symbolic Execution Rules
We derive these rules from the relational semantics. We assume  has the form as above, with
has the form as above, with  .
.
Assignment
Given assignment

where  is an expression, change
is an expression, change  into
into  interpreted in the current state, obtaining
interpreted in the current state, obtaining
![Equation \begin{equation*}
x = f[x:=e_x,y:=e_y]\ \land y = e_y \land P_C
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img9a1d83f0d08f947ac87fb390ba7656d9.png)
How does this follow from relation composition?
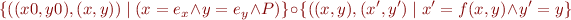
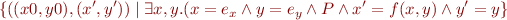
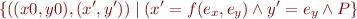
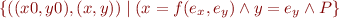
Assume
Given assume statement

add  to path condition, obtaining
to path condition, obtaining
![Equation \begin{equation*}
x = e_x \land y = e_y \land\ (P_C \land F[x:=e_x, y:=e_y])
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img839138b5713a846d469274578ffc92ef.png)
Havoc
Given havoc statement:

change  into a fresh variable:
into a fresh variable:
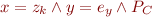
where  is a fresh variable (implicitly
is a fresh variable (implicitly  -quantified).
-quantified).
Assert
Given

prove the condition:
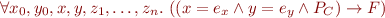
(or save this condition as a conjunct in the final verification condition).
Justification: note that the postcondition at current program point is

so the above statement expresses the condition that the assertion will hold starting from all initial states.
Weakening Optionally, after assert(F), symbolic execution can execute
havoc(x) havoc(y) assume(F)
which essentially has the effect of obtaining
![Equation \begin{equation*}
x = x_k \land y = y_k \land F[x:=x_k, y:=y_k]
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img492fae8fc1ce1d923ed2c325c19f5a4a.png)
where  ,
, 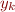 are fresh variables and where
are fresh variables and where
![Math $F[x:=x_k, y:=y_k]$](/w/lib/exe/fetch.php?media=wiki:latex:/imgbabdac6152b4de790ec7618594b322ff.png) becomes the new path condition. This means that only information about
the assertion is propagated further, other information about the past is forgotten.
becomes the new path condition. This means that only information about
the assertion is propagated further, other information about the past is forgotten.
Sequential composition
This is handled implicitly: execute statements one by one.
Non-deterministic choice
Execute both branches and collect proof obligations from both branches.
Exponential explosion remedy:
- work on control-flow graph
- merge symbolic states when edges merge
Merging: Given two symbolic states:
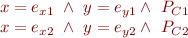
generate a merged symbolic state
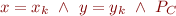
where 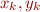 are fresh variables, and where
are fresh variables, and where 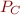 is
is
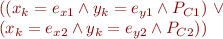
Then continue symbolic execution from this state.
Important Optimizations
Expression Simplification
Simplification: if we can simplify symbolic expressions
 ,
, 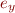 or path condition
or path condition 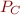 , this can be very
useful, especially if the size of the expression decreases.
, this can be very
useful, especially if the size of the expression decreases.
An important special case is constant folding. Example: if  is
is 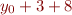 , we replace it by
, we replace it by  .
.
Much more sophisticated simplifications are possible (e.g. keep polynomials in normal form, apply terminating rewrite rules); see the references at the end of page.
Path Pruning
If the path condition formula 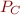 becomes unsatisfiable, the relation is empty and symbolic execution can stop (path is unreachable).
becomes unsatisfiable, the relation is empty and symbolic execution can stop (path is unreachable).
Special case: if the initial condition specifies values of variables, then we know which branch to enter, and symbolic execution reduces to concrete execution (interpreter for the programming language).
Approximation in Symbolic Execution
Instead of computing exact relation, we can compute approximate relation for the program. Two main approaches:
- larger relation: overapproximation (safe approximation)
- smaller relation: underaproximation (used for bug finding, sometimes it's not guaranteed to be smaller or bigger)
Why we approximate:
- ensure termination even for programs that have loops
- can still obtain useful information about the program
We can do approximation by modifying the current symbolic execution formula to be
- stronger (for under-approximation)
- weaker (for over-approximation)
We will study this topic in the rest of the course under the framework of abstract interpretation.
In terms of symbolic execution, these can often be described by imposing a stronger normal form on the formula 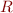 of symbolic execution.
of symbolic execution.
Over-Approximation
Creates weaker formulas, which are guaranteed to be of stronger form. Here are some examples of how normal form for 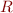 looks in that case. Key question is how to ensure that the formulas look like this–it means that we need to modify propagation rules to generate as strong as possible formulas in this normal form.
looks in that case. Key question is how to ensure that the formulas look like this–it means that we need to modify propagation rules to generate as strong as possible formulas in this normal form.
Sign Analysis
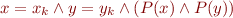
where 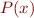 is one of the formulas
is one of the formulas  ,
,  ,
,  (and similarly for
(and similarly for 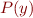 )
)
Interval Analysis
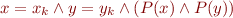
where 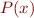 is a formula of the forms
is a formula of the forms  ,
,  ,
,  , or
, or 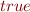 (analogously for
(analogously for  )
)
Linear or Polynomial Constraint Analysis
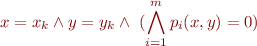
where 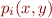 are polynomials of degree
are polynomials of degree  . For
. For  we obtain systems of linear constraints.
we obtain systems of linear constraints.
Ensuring termination of the analysis in the presence of loops:
- we check whether we have seen a weaker symbolic state before, if we have, then we stop
- we design normal forms of
 so that the number of iterations through loops is always finite
so that the number of iterations through loops is always finite
We look at these topics when we study abstract interpretation and data-flow analysis.
Over-Approximation Using Supplied Asserts
Approach two: interpreting assert(P) as:
assert(P) havoc(x,y) assume(P)
which is an over-approximation. To see this, we need to give a relational meaning to assert, which we do next. The advantage is that, if asserts express correct loop invariants, this over-approximation will terminate and prove the desired assertions. We can ensure termination by providing a correct assert in each cycle of the control-flow graph.
Under-Approximations
Creates stronger formulas than formulas representing program meaning.
- can often be expressed as adding certain 'assume' statements
If the first statements are
assume (x=0) assume (x=1)
Then symbolic execution knows the exact values and can work as an interpreter.
- simplification optimization computes the exact values of variables
There are techniques that do under-approximation by selecting values of certain variables.
- find a satisfying assignment for
 , take value
, take value  of
of  in it and replace
in it and replace  with
with 
Other techniques for underapproximation:
- Bounding depth: stop executing for paths longer than some value
- Bounding state: small integer width, small number of objects in heap
- Loop unrolling: replace loop( c ) with c[]c;c[]c;c;c for some number of times
References
- Symbolic execution and program testing by James C. King (pdf) (1976)
- Lori Clarke and Debra Richardson: Symbolic Evaluation Methods for Program Analysis, in Program Flow Analysis: Theory and Applications, Prentice-Hall 1981.