Chaotic Iteration in Abstract Interpretation: How to compute the fixpoint?
In Abstract Interpretation Recipe, note that if the set of program points is  , then we are solving the system of eqautions in
, then we are solving the system of eqautions in  variables
variables 
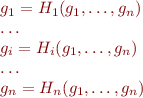
where

The approach given in Abstract Interpretation Recipe computes in iteration  values
values  by applying all equations in parallel to previous values:
by applying all equations in parallel to previous values:
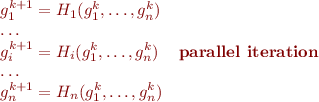
What happens if we update values one-by-one? Say in one iteration we update  -th value, keeping the rest same:
-th value, keeping the rest same:
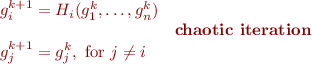
here we require that the new value 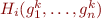 differs from the old one
differs from the old one 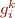 . An iteration where at each step we select some equation
. An iteration where at each step we select some equation  (arbitrarily) is called chaotic iteration. It is abstract representation of different iteration strategies.
(arbitrarily) is called chaotic iteration. It is abstract representation of different iteration strategies.
Questions:
- What is the cost of doing one chaotic versus one parallel iteration? (chaotic is
 times cheaper)
times cheaper) - Does chaotic iteration converge if parallel converges?
- If it converges, will it converge to same value?
- If it converges, how many steps will convergence take?
- What is a good way of choosing index
 (iteration strategy), example: take some permutation of equations. More generally: fair strategy, for each vertex and each position in the sequence, there exists a position afterwards where this vertex is chosen.
(iteration strategy), example: take some permutation of equations. More generally: fair strategy, for each vertex and each position in the sequence, there exists a position afterwards where this vertex is chosen.
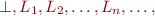 be vectors of values
be vectors of values  in parallel iteration and
in parallel iteration and
 be vectors of values
be vectors of values  in chaotic iteration
in chaotic iteration
These two sequences are given by monotonic functions 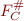 and
and 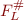 and the second one is clearly smaller i.e.
and the second one is clearly smaller i.e.

Compare values 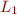 ,
,  , …,
, …, 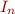 ,
,  in the lattice:
in the lattice:
 , generally
, generally  (proof by induction)
(proof by induction)- when selecting equations by fixed permutation
 , generally
, generally 
Therefore, using the Lemma from Comparing Fixpoints of Sequences twice, we have that these two sequences converge to the same value.
Worklist Algorithm and Iteration Strategies
Observation: in practice 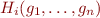 depends only on small number of
depends only on small number of 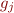 , namely predecessors of node
, namely predecessors of node  .
.
Consequence: if we chose  , next time it suffices to look at successors of
, next time it suffices to look at successors of  (saves traversing CFG).
(saves traversing CFG).
This leads to a worklist algorithm:
- initialize lattice, put all CFG node indices into worklist
- choose
 , compute new
, compute new  , remove
, remove  from worklist
from worklist - if
 has changed, update it and add to worklist all
has changed, update it and add to worklist all 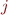 where
where 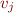 is a successor of
is a successor of 
Algorithm terminates when worklist is empty (no more changes).
Useful iteration strategy: reverse postorder and strongly connected components.
Reverse postorder: follow changes through successors in the graph.
Strongly connected component (SCC) of a directed graph: path between each two nodes of component.
- compute until fixpoint within each SCC
If we generate control-flow graph from our simple language, what do strongly connected components correspond to?
References
- Principles of Program Analysis Book, Chapter 6