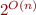Summary of Hoare Logic
Summary of Proof Rules
We next present (one possible) summary of proof rules for Hoare logic.
Weakening and Strengthening
Strengthening precondition:
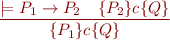
Weakening postcondition:
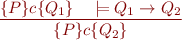
Loop Free Blocks
We can directly use rules we derived in lecture04 for basic loop-free code. Either through weakest preconditions or strongest postconditions.
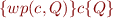
or,
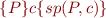
For example, we have:
![Equation \begin{equation*}\begin{array}{l}
\{Q[x:=e]\}\ (x=e)\ \{Q\} \\
\ \\
\{\forall x.Q\}\ {\it havoc}(x)\ \{Q\} \\
\ \\
\{P\}\ assume(F)\ \{P \land F\}
\end{array}
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img8b730781d2150b2c3cf22dcdb9622b20.png)
Loops

Sequential Composition
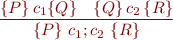
Non-Deterministic Choice
![Equation \begin{equation*}
\frac{\{P\} c_1 \{Q\} \ \ \ \{P\} c_2 \{Q\}}
{\{P\} c_1 [] c_2 \{Q\}}
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/imgcdb1e04fe7e0f81d6ff0c59c877d865b.png)
Applying Proof Rules given Invariants
Let us treat 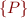 as a new kind of statement, written
as a new kind of statement, written
assert(P)
For the moment the purpose of assert is just to indicate preconditions and postconditions. When we write
assert(P) c1; assert(Q) c2; assert(R)
we expect that these Hoare triples hold:
{P} c1 {Q}
{Q} c2 {R}
Consider control-flow graph of a program with statements assert,assume,x=e and with graph edges expressing “[]” and “;”.
We will say that the program  is sufficiently annotated iff
is sufficiently annotated iff
- the first statement is assert(Pre)
- the last statement is assert(Post)
- every cycle in the control-flow graph contains at least one assert
An assertion path is a path in its control-flow graph that starts and ends with assert. Given assertion path
assert(P) c1 ... cK assert(Q)
we omit any assert statements in the middle, obtaining from c1,…,cK statements d1,…,dL. We call
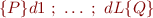
the Hoare triple of the assertion path.
A basic path is an assertion path that contains no assert commands other than those at the beginning and end. Each sufficiently annotated program has finitely many basic paths.
Theorem: If Hoare triple for each basic path is valid, then the Hoare triple 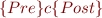 is valid.
is valid.
Proof: If each basic path is valid, then each path is valid, by induction and Hoare logic rule for sequential composition. Each program is union of (potentially infinitely many) paths, so the property holds for the entire program. (Another explanation: consider any given execution and corresponding path in the control-flow graph. By induction on the length of the path we prove that all assert statements hold, up to the last one.)
The verification condition of a basic path is the formula whose validity expresses the validity of the Hoare triple for this path.
Simple verification conditions for a sufficiently annotated program is the set of verification conditions for each each basic path of the program.
One approach to verification condition generation is therefore:
- start with sufficiently annotated program
- generate simple verification conditions
- prove each of the simple verification conditions
In a program of size  , what is the bound on the number of basic paths?
, what is the bound on the number of basic paths?
Further reading
- Calculus of Computation Textbook, see Section 5.2: Partial Correctness
- Glynn Winskel: The Formal Semantics of Programming Languages, fourth printing, MIT Press, 1997, see Section 7.4: Verification Conditions