Satisfiability of Sets of Formulas
We next introduce sets of formulas as a way of talking about potentially infinite conjunctions of formulas. We will need this when reducing reasoning in first-order logic to reasoning in propositional logic.
We say that interpretation  is a model for a set of formulas
is a model for a set of formulas  , written
, written  , iff for each
, iff for each 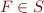 ,
,  . In other words, we view a set of formulas as a (potentially infinite) conjunction; when
. In other words, we view a set of formulas as a (potentially infinite) conjunction; when  is finite then
is finite then  is the same condition as
is the same condition as 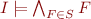 .
.
Example: the set 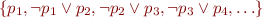 is an infinite satisfiable set. The example of one satisfying interpretation is the interpretation which evaluates all variables to
is an infinite satisfiable set. The example of one satisfying interpretation is the interpretation which evaluates all variables to 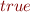 .
.
Clearly, if  and
and  , then also
, then also 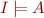 .
.
We say that a set of formulas  is satisfiable iff there exists an interpretation
is satisfiable iff there exists an interpretation  such that
such that  .
.