QBF and Quantifier Elimination
Quantified Propositional Formula Syntax
We extend the definition of formulas with quantifiers  and
and 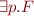 where
where  :
:
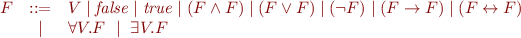
Eliminating quantifiers by expansion
We can apply the following rules to eliminate propositional quantifiers:
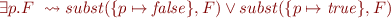
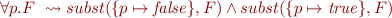
Note that the expansion can produce exponentially larger formula.
Notion of quantifier elimination applies to other logic as well.
Definition: A logic has quantifier elimination if for every formula in the logic, there exists an equivalent formula without quantifiers.
Definition: A quantifier elimination algorithm is an algorithm that takes a formula in a logic and converts it into an equivalent formula without quantifiers.
Observation: Formula  is valid iff
is valid iff  is true.
is true.
Observation: Formula  is satisfiable iff
is satisfiable iff 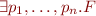 is true.
is true.
In general QBF formulas can have alternations between  and
and  quantifiers:
quantifiers:
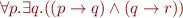
Quantified Propositional Formula Semantics
We can similarly provide recursive semantic function definition for propositional logic.
Summary of Computational Complexity of Problems
- checking satisfiability of propositional formula
 is NP-complete
is NP-complete - checking validity of propositional formula
 is coNP-complete
is coNP-complete - checking truth value of arbitrary QBF formula is PSPACE-complete