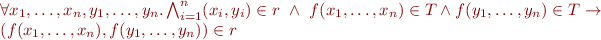Partial Congruences
Instead of a congruence on the (typically infinite) set of all ground terms we will compute congruences on a given finite set of ground terms. We call these congruences partial congruences; they are simply congruences on a subset of the original set.
Theorem: Let  be a set of ground terms and
be a set of ground terms and  a congruence on
a congruence on  . Then
. Then 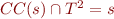 where
where  denotes the congruence closure of
denotes the congruence closure of  .
.
Proof:
Show 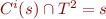 for all
for all  , by induction.
, by induction.
 : s = s
: s = s
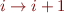 :
:
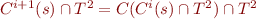 , by induction hypothesis
, by induction hypothesis 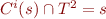 .
Thus
.
Thus 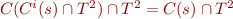 .
As
.
As  adds only needed term for congruence, the added term are either not in
adds only needed term for congruence, the added term are either not in  or
or  in not a congruence.
By hypothesis
in not a congruence.
By hypothesis  is a congruence, so
is a congruence, so 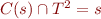 .
Therefore
.
Therefore 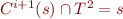 .
.
Proof End.
When checking a formula we compute congruences on a finite set of terms that occur in the formula.
We apply the congruence condition only to terms that already exist in the set, using congruence condition: