Herbrand Universe for Equality
Recall example of formula  :
:
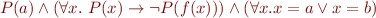
Replace '=' with 'eq':
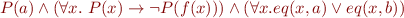
call the resulting formula  .
.
Consider Herbrand model 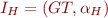 for the set
for the set 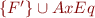 . The relation
. The relation 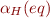 splits
splits  into two sets: the set of terms eq with
into two sets: the set of terms eq with  , and the set of terms eq with
, and the set of terms eq with  . The idea is to consider these two partitions as domain of new interpretation, denoted
. The idea is to consider these two partitions as domain of new interpretation, denoted ![Math $([GT], \alpha_Q)$](/w/lib/exe/fetch.php?media=wiki:latex:/img3817ed31e41b38cc0f466bbcb61a9e96.png) .
.
Constructing Model for Formulas with Equality
Let  be a set of formulas in first-order logic with equality and
be a set of formulas in first-order logic with equality and 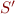 result of replacing '=' with 'eq' in
result of replacing '=' with 'eq' in  . Suppose
. Suppose 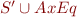 is satisfiable.
is satisfiable.
Let 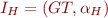 be Herbrand model for
be Herbrand model for 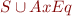 . We construct a new model as Interpretation Quotient Under Congruence of
. We construct a new model as Interpretation Quotient Under Congruence of 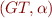 under congruence 'eq'. Denote quoient structure by
under congruence 'eq'. Denote quoient structure by ![Math $I_Q = ([GT],\alpha_Q)$](/w/lib/exe/fetch.php?media=wiki:latex:/img5a91e94195aaa1d6b6ceb515d14bb401.png) . By theorem on quotient structures,
. By theorem on quotient structures,  is true in
is true in  . Therefore,
. Therefore,  is satisfiable.
is satisfiable.
Herbrand-Like Theorem for Equality
Theorem: For every set of formulas with equality  the following are equivalent
the following are equivalent
 has a model;
has a model; has a model whose domain is the quotient
has a model whose domain is the quotient ![Math $[GT]$](/w/lib/exe/fetch.php?media=wiki:latex:/imgee416c221e0f04a2fc4dea4cad69ad89.png) of the set of ground terms under some congruence.
of the set of ground terms under some congruence.
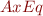 are
are