DPLL Algorithm for SAT
Approach:
- boolean constraint propagation when possible
- case analysis on variables for completeness
INPUT: set of clauses  (see Normal Forms for Propositional Logic, Definition of Propositional Resolution)
(see Normal Forms for Propositional Logic, Definition of Propositional Resolution)
OUTPUT: true iff there exists an interpretation that makes  true
true
Terminology
A unit clause is 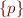 or
or 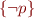 where
where  .
.
Unit resolution is application of resolution to two clauses where at least one clause is a unit clause.
- like substituting the value of variable forced by the unit clause
Boolean Constraint Propagation
Apply unit resolution as much as possible.
def BCP(S : Set[Clause]) : Set[Clause] = if for some unit clause U and clause C in S, resolve(U,C) is not in in S then BCP(S union resolve(U,C)) else S
Note: for each unit clause and other clause we can perform unit resolution at most once (variable disappears)
- BCP is polynomial procedure
We do not need to keep literals that are subset of existing ones:
def RemoveSubsumed(S : Set[Clause]) : Set[Clause] =
if there are C1,C2 in S such that C1 subset C2
then RemoveSubsumes(S - {C2})
else S
In particular, when we apply unit resolution, the original clause can be deleted.
DPLL Recursively
def DPLL(S : Set[Clause]) : boolean =
val S' = RemoveSubsumed(BCP(S))
if (emptyClause in S') then false
else if (S' has only unit clauses) then true
else
val P = pick variable from FV(S')
DPLL(F' union {p}) or DPLL(F' union {Not(p)})
State Representation
State representation - group clauses by number of elements:
- S.C (conflict, size zero): true if empty clause was derived
- S.A (assignment, size one): partial map from
 to
to 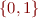
 for
for 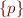
 for
for 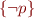
- S.B: the remaining clauses
To check satisfiability of set of clauses, invoke DPLL procedure with
- S.C=false
- S.A=EmptyMap
- S.B containing all desired clauses
Desired invariants:
- if S.A(p) defined, then p does not occur in S.B
- S.B has only clauses with at least two literals
Maintaining invariant - part of BCP
- if S.A(p)=1, delete from S.B clauses containing
 and remove literals
and remove literals  from clauses in S.B
from clauses in S.B - if S.A(p)=0, delete from S.B clauses containing
 and remove literals
and remove literals  from clauses in S.B
from clauses in S.B - if empty clause is in S.B, set S.C to true
- if
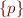 is in S.B, then set
is in S.B, then set 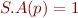
- if
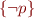 is in S.B, then set
is in S.B, then set 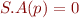
Termination conditions (when invariants hold):
- if S.C, set is unsatisfiable
- if S.B is empty and not S.C, then S.A gives satisfying assignment
Emiting a Satisfying Assignments or a Proof
Instead of returning just true/false we want SAT solver to return
- one satisfying assignment, if
 is satisfiable (easy: print S.A)
is satisfiable (easy: print S.A) - proof, if
 is unsatisfiable - in some format
is unsatisfiable - in some format
Emiting resolution proofs - needs extra work
Unit resolution is resolution, so we can construct proofs directly.
Decision step (picking variable value): from proofs for
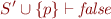
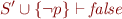
we would like to construct the proof for
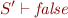
From
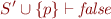
derive proof tree for
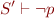
and from
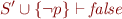
derive proof tree for
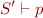
Then combine these two trees with resolution on 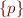 and
and 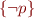 to get
to get 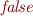 .
.
Why can we modify resolution proof to move  from assumption and put its negation to conclusion?
from assumption and put its negation to conclusion?
Lower Bounds on Running Time
Observation: constructed resolution proof is polynomial in the running time of the DPLL algorithm.
Theorem: for some formulas, shortest resolution proofs are exponential.
This does not contradict that P vs NP question is open, because there may be “better” proof systems than resolution.
Lower bounds for both resolution and a stronger system are shown here by proving that interpolants can be exponential, and that interpolants are polynomial in proof size (see Interpolants from Resolution Proofs):