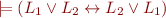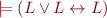Definition of Propositional Resolution
Recall:
- literal is a propositional variable
 or its negation
or its negation  .
. - clause is a disjunction of literals
Clauses as Sets of Literals
The order and the number of occurrences of literals in clauses do not matter, because of these valid formulas:
We therefore represent clauses as sets of literals. For example, we represent the clause  as the set
as the set 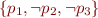 . We represent false as an empty clause and we do not represent true.
. We represent false as an empty clause and we do not represent true.
Resolution Rule
Viewing clauses as sets, propositional resolution is the following rule:
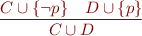
Here  are clauses and
are clauses and  is a propositional variable.
is a propositional variable.
Intuition: consider equivalent formulas
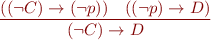
Applying Resolution Rule to Check Satisfiability
Steps:
- If we wish to check validity, negate the formula. From now on, assume we are checking satisfiability.
- Convert formula into polynomially large equisatisfiable formula in conjunctive normal form (see Normal Forms for Propositional Logic)
- Keep applying resolution rule until either
- empty clause
 is derived
is derived - application of the resolution rule produces no new clauses
Soundness of Resolution Rule
Suppose that  and
and 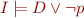 . If
. If 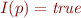 , then from
, then from 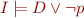 we conclude
we conclude  and therefore
and therefore  . Similarly, if
. Similarly, if 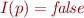 , then from
, then from  we conclude
we conclude  and therefore
and therefore  .
.
Therefore, if  and
and  is the result of applying resolution rule to
is the result of applying resolution rule to 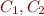 , then
, then  if and only if
if and only if 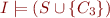 . Consequently, if we obtain an empty clause (false) by applying resolution, then the original set is not satisfiable either.
. Consequently, if we obtain an empty clause (false) by applying resolution, then the original set is not satisfiable either.