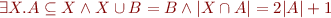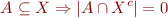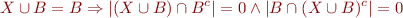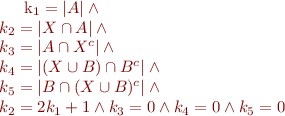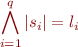Deciding Boolean Algebra with Presburger Arithmetic
Motivation
Definition of BAPA
See Figure 3 on page 5 of the paper and compare to its special cases: BA and PA.
Semantics: we consider the theory of models where integers are interpreted as integers and sets are interpreted as subsets of some finite set. For each finite set we have one interpretation. (If we prove a valid formula, it will hold for arbitrarily large finite universes.) 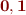 are empty and universal set. We interpret constant
are empty and universal set. We interpret constant  as
as  .
.
Example
Simplifying Atomic Formulas
For sets  :
:
 becomes
becomes 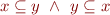
 becomes
becomes 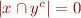
Result: all set variables and operators occur within  formula where
formula where  is expression built from set variables,
is expression built from set variables, 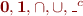 .
.
Transform  into union of disjoint Venn regions. Let
into union of disjoint Venn regions. Let  be all set variables. Venn regions are connected regions in the Venn diagram, and are analogous to conjunctive normal form:
be all set variables. Venn regions are connected regions in the Venn diagram, and are analogous to conjunctive normal form:
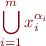
where  is either
is either  or
or  (complement of
(complement of  ).
).
Now observe that each set expression  is a disjoint union of certain Venn regions. It is union of precisely those regions that belong to disjunctive normal form of the corresponding propositional formula.
is a disjoint union of certain Venn regions. It is union of precisely those regions that belong to disjunctive normal form of the corresponding propositional formula.
Then use

We therefore assume that the only occurence of sets and set operators is within  where
where  is a Venn region.
is a Venn region.
Separating BA and PA Part
Transform formula to prenex form
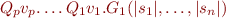
where  is quantifier-free.
is quantifier-free.
For each expression  in
in 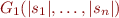 introduce a fresh variable
introduce a fresh variable  that denotes the value
that denotes the value  . We obtain
. We obtain
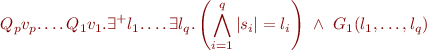
Note that 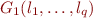 is a quantifier-free PA formula.
is a quantifier-free PA formula.
Here 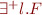 denotes
denotes  .
.
We will eliminate integer and set quantifiers from the entire subformula 
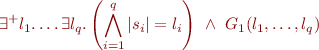
Indeed, we can always transform this formula to a quantifier-free formula by substituting  back into
back into  .
.
In which parts of this formula do we find variables  that we wish to eliminate
that we wish to eliminate
Eliminating Quantifiers
Eliminating Integer Existential
Eliminating Set Existential
Lemma:
Let 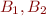 be two finite disjoint sets and
be two finite disjoint sets and 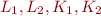 non-negative integers. Then the following two conditions are equivalent:
non-negative integers. Then the following two conditions are equivalent:
- there exists a finite set
 such that:
such that: 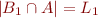 ,
, 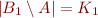 ,
, 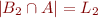 , and
, and 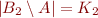 ;
; 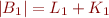 and
and 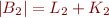 .
.
Eliminating Universals
Express them using negation and existentials.



 from the following formula:
from the following formula: