Describing Reachable States using Collecting Semantics
Main question: What values can variables of the program take at different program points?
We can represent programs by control-flow graphs (CFG).
Definition: Control flow-graph is a graph with nodes  , edges
, edges 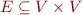 and for each edge
and for each edge  a command given by relation
a command given by relation 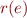 , with initial
, with initial  and final node
and final node 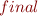
Program points are CFG nodes. Statements are labels on CFG edges.
We look at a particular way of representing and computing sets of reachable states, splitting states by program counter (control-flow graph node): collecting semantics.
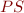 - states describing values of program variables (not including program counter).
- states describing values of program variables (not including program counter).
For each program point  , we have the set of reachable states
, we have the set of reachable states 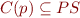 .
.
The set of all reachable states of the program is 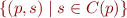 .
.
Let  be initial program counter and
be initial program counter and  the set of values of program variables in
the set of values of program variables in  .
.
The set of reachable states is defined as the least solution of constraints:

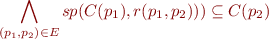
over variables 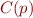 for all of finitely many program points
for all of finitely many program points  .
.
The last condition is equivalent to
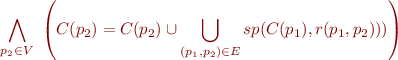
Here 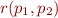 is the relation giving semantics for the command associated with edge
is the relation giving semantics for the command associated with edge 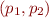 .
.
Set of recursive inequations in the lattice of products of sets. Note 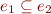 is equivalent to
is equivalent to  , so we have equations in lattice.
, so we have equations in lattice.
They specify function  from pairs of sets of states to pairs of sets of states which is
from pairs of sets of states to pairs of sets of states which is  -morphism (and therefore monotonic).
-morphism (and therefore monotonic).
Least fixpoint of  is
is 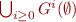 .
.
Example
Sets of states at selected points:
i = 20;
x = 2;
while (i > 0) {
x = x + 4;
i = i - 1;
}
if (x==0) {
error;
} else {
y = 1000/x;
}
After the assignment of  to 2, the set of reachable states
to 2, the set of reachable states  is
is