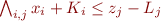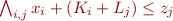This is an old revision of the document!
Simple QE for Integer Difference Inequalities
Language of Less-Than-Equals Over Integers
Consider language: 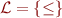 and the theory of structure
and the theory of structure  where
\[
where
\[
\alpha({\le}) = \{ (x,y) \mid x \le y \}
\]
Lemma: This theory does not admit quantifier elimination.
Proof.
Suppose the theory admits quantifier elimination.
End.
So  must be expressible. Let us extend the language: consider theory in language
must be expressible. Let us extend the language: consider theory in language 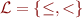 with
with  interpreted as
interpreted as  on integers.
on integers.
Does the theory of this structure admit quantifier elimination?
Extending the Language
Language: 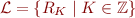
Theory of structure  where
\[
where
\[
\alpha(R_K) = \{ (x,y) \mid x + K \leq y \}
\]
Note that 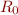 is the less-than-equal relation on integers.
is the less-than-equal relation on integers.
In other words, we look at the language of this syntax, where  is the set of variables:
is the set of variables:
F ::= A | (F&F) | (F|F) | ~F | ALL V.F | EX V.F A ::= v=v | v + K ≤ v | true | false K ::= ... -2 | -1 | 0 | 1 | 2 | ...
Quantifier Elimination in the Extended Language
Quantifier elimination for this language is similar to Simple QE for Dense Linear Orders.
What are conjunctions of literals equivalent to?
How do we eliminate existential quantifier?
Example
Prove:
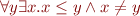
++|

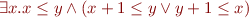

Because there are no lower or upper bounds, these formulas are 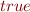
If we apply this technique to a closed formula in this theory, what formulas do we obtain as a result?
 .
So it must be built out of atomic formulas
.
So it must be built out of atomic formulas  and
and  , and is therefore either true or false.
, and is therefore either true or false.
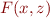 equivalent to
\[
equivalent to
\[
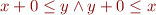
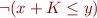 equivalent to?
equivalent to?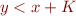

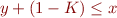
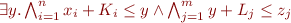
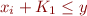 and
and