This is an old revision of the document!

Mapping Fixpoints Under Lattice Morphisms

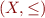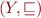Definition: Let $(X,\le)$ and $(Y,\sqsubseteq)$ be complete lattices. We call 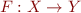$F : X \to Y$ a complete join-morphism iff for each set $X_1 \subseteq X$ we have \[

 F(\sqcup X_1) = \sqcup \{ F(a).\ a \in X_1 \}

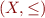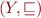Lemma: Let $(X,\le)$ and $(Y,\sqsubseteq)$ be complete lattices, and 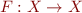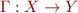$F : X \to X$ , $\Gamma : X \to Y$ , $F^\# : Y \to Y$ be complete morphisms (they distribute through arbitrary least upper bound) such that \[

  F(\Gamma(y)) \le \Gamma(F^\#(y))

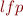\] for all $y \in Y$ . If $lfp$ denotes least fixpoint of a function, then \[

  lfp(F) \le \Gamma(lfp(F^\#))

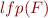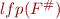In other words, we can approximate $lfp(F)$ by computing $lfp(F^\#)$ .