This is an old revision of the document!
Correctness of A/G Reasoning
Correctness as Approximation of Relations
Specification  provides a relation that is intended to approximate relation
provides a relation that is intended to approximate relation  defining the meaning of procedure, that is, we would like to prove
\[
defining the meaning of procedure, that is, we would like to prove
\[
r \subseteq s
\]
Following Relational Semantics of Procedures, consider one procedure and its associated function \[
m : {\cal R} \to {\cal R}
\]
and its fixed point  .
.
The idea of approach based on specifications is to prove that, if we assume that procedure calls satisfy the specification, then we can prove the specification for the procedure we are verifying. In other words, specifications provide a relation  such that
\[
such that
\[
m(s) \subseteq s
\]
We claim that  where
where 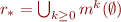 .
.
Proof:
Expressing Approximation Using Assume and Assert
Consider a program with only one state variable  .
.
We express our approximation as \[
\begin{array}{l}
assert\, (P(x));\\
havoc(x); \\
assume(Q(x))
\end{array}
\]
So, we would like to show that \[
r\qquad \subseteq\qquad
\begin{array}{l}
(assert\, (P(x));\\
havoc(x); \\
assume\, (Q(x)))
\end{array}
\] is implied by the condition we are checking: \[
\begin{array}{l}
(assume\, (P(x));\\
r; \\
assert\, (Q(x)))
\end{array}
\qquad\subseteq \qquad
havoc(x)
\]
Shunting rules
For relations  ,
,  that propagate errors (as in Assert and error conditions):
\[
that propagate errors (as in Assert and error conditions):
\[
(assume(P(x)); r \subseteq s)\ \ \leftrightarrow\ \ r \subseteq assert(P(x)); s
\] \[
(r; assert(Q(x)) \subseteq s)\ \ \leftrightarrow\ \ r \subseteq s;assume(Q(x))
\]
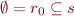 , and by monotonicity of
, and by monotonicity of  we obtain that
we obtain that  implies
implies 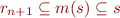 . Therefore,
. Therefore,  , so
, so  ) we can show by induction starting from innermost call. The innermost call has no recursive invocation, so it presents the base case of induction.
) we can show by induction starting from innermost call. The innermost call has no recursive invocation, so it presents the base case of induction.