This is an old revision of the document!
Compositional VCG
Let 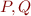 be formulas and
be formulas and  a command of our language using variables
a command of our language using variables 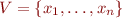 . To check
. To check 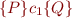 we compute formula
we compute formula  containing
containing
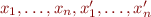 specifying the semantics of c_1, that is, formula
specifying the semantics of c_1, that is, formula  such that
\[
such that
\[
r_c(c_1) = \{ (\{("x_1",x_1),\ldots,("x_n",x_n)\},\{("x_1",x'_1),\ldots,("x_n",x'_n)\}) \mid F_1 \}
\]
Denote the truth value of formula in two states by 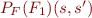 (predicate for the formula) using an auxiliary definition of
(predicate for the formula) using an auxiliary definition of 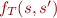 (function for the term):
\[
\begin{array}{l}
(function for the term):
\[
\begin{array}{l}
P_F(F_1 \land F_2)(s,s') = P_F(F_1)(s,s') \land P_F(F_2)(s,s') \\ P_F(F_1 \lor F_2)(s,s') = P_F(F_1)(s,s') \lor P_F(F_2)(s,s') \\ P_F(\lnot F_1)(s,s') = \lnot P_F(F_1)(s,s') \lor P_F(F_2)(s,s') \\ P_F(t_1 = t_2)(s,s') = (f_T(t_1)(s,s') = f_T(t_2)(s,s')) \\ P_F(t_1 < t_2)(s,s') = (f_T(t_1)(s,s') < f_T(t_2)(s,s')) \\ f_T(t_1 + t_2)(s,s') = f_T(t_1)(s,s') + f_T(t_2)(s,s') \\ f_T(t_1 - t_2)(s,s') = f_T(t_1)(s,s') - f_T(t_2)(s,s') \\ f_T(K * t_1)(s,s') = K \cdot f_T(t_1)(s,s') \\ f_T(x)(s,s') = s(x) \\ f_T(x')(s,s') = s'(x)
\end{array} \]
Then we can construct formula  such that
such that 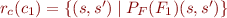 . Denote such formula
. Denote such formula  by
by 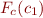 .
To can then represent the validity of a Hoare triple
\[
.
To can then represent the validity of a Hoare triple
\[
\forall s,s'.\ (f_T(P)(s) \land (s,s') \in r_c(r) \rightarrow f_T(Q))
\] by formula \[
\forall x_1,\ldots,x_n,x'_1,\ldots,x'_n.\ (P \land F_c(c_1) \rightarrow Q)
\]
Rules for Computing Formulas for Commands
Therefore, to prove Hoare triples, we just need to compute for each command  the formula
the formula 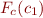 . We next show how to do it. These rules all follow from the semantics of our language.
. We next show how to do it. These rules all follow from the semantics of our language.
Assignment
\[
F_c(x=e) = (x'=e \land \bigwedge_{v \in V \setminus \{x\}} v=v')
\]
Assume
\[
F_c({\it assume}(e)) = (e \land \bigwedge_{v \in V} v=v')
\]
Havoc
\[
F_c({\it havoc}(x)) = (\bigwedge_{v \in V \setminus\{x\}} v=v')
\]
For simplicity of notation, in the sequel we work with state that has only one variable, x.
Union
Note \[
\{(x,x') \mid F_1 \} \cup \{(x,x') \mid F_2 \} = \{(x,x') \mid F_1 \lor F_2 \}
\] Therefore, \[
F_c(c_1 [] c_2) = F_c(c_1) \lor F_c(c_2)
\]
Sequential composition
Note that \[
\{(x,x') \mid F_1 \} \circ \{(x,x') \mid F_2 \} = \{ (x,z) \mid F_1[x':=z] \} \circ \{ (z,x') \mid F_2[x:=z] \} = \{ (x,z) \mid \exists z. F_1[x':=z] \land F_2[x:=z] \}
\] Therefore, \[
F_c(c_1\ ;\ c_2)\ =\ (\exists z. F_c(c_1)[x':=z] \land F_c(c_2)[x:=z])
\]
To avoid re-using variables, introduce always a fresh variable as z, denote it  .
.
Using Computed Formulas
Note: the result will be disjunctions of such existential quantifications. We can always move them to top level.
Resulting formula: \[
\forall x,x'.\ (P \land (\exists z_1,\ldots,z_n. F_c(c_1))\ \rightarrow Q)
\] which is equivalent to \[
\forall x,x',z_1,\ldots,z_n. (P \land F_c(c_1) \rightarrow Q)
\]
Conclusions: we can just generate fresh variables for intermediate points and prove the validity of the resulting quantifier free formula 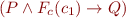 .
.
Optimizations: assignments and assume statements generate equalities, many of which can be eliminated by one-point rule \[
(\exists x. x=t \land F(x)) \leftrightarrow F(t)
\]
Example
Take the program in the example below:
(if (x < 0) x=x+1 else x=x); (if (y < 0) y=y+x else y=y);
It translate into the following relation:
\[
\begin{array}{l}
(assume(x<0) \circ (x = x+1)\ \cup\ assume (\lnot (x<0)) \circ skip) \circ
(assume(y<0) \circ (y = y+x)\ \cup\ assume(\lnot(y<0)) \circ skip)
\end{array}
\]
By distribution of composition over union the relation above becomes:
\[
\begin{array}{l}
(assume(x<0) \circ (x = x+1) \circ assume(y<0) \circ (y = y+x)) \cup
(assume (\lnot (x<0)) \circ assume(y<0) \circ (y = y+x)) \cup
(assume(x<0) \circ (x = x+1) \circ assume(\lnot(y<0))) \cup
(assume (\lnot (x<0)) \circ assume(\lnot(y<0)))
\end{array}
\]
It can be easily proven that  :
\[
\begin{array}{1}
\{P\}\ \cup_i p_i\ \{Q\} \Leftrightarrow
:
\[
\begin{array}{1}
\{P\}\ \cup_i p_i\ \{Q\} \Leftrightarrow
sp(P, \cup_i p_i) \subseteq Q \Leftrightarrow
\cup_i sp(P, p_i) \subseteq Q \Leftrightarrow
\wedge_i sp(P,p_i) \subseteq Q \Leftrightarrow
\wedge_i \{P\}\ p_i\ \{Q\}
\end{array}
\]
We can take all the terms of the union one by one as in the following small example:
\[
\begin{array}{1}
(assume(x<0) \circ (x = x+1) \circ assume(y<0) \circ (y = y+x)) \cup
assume(\lnot (x<0)) \Leftrightarrow
\exists x_1,y_1.(x<0 \wedge y_1 = y \wedge x_1 = x) \wedge (x'=x_1 + 1 \wedge y'=y_1)) \vee
(\lnot (x<0) \wedge x'=x \wedge y'=y)
\end{array}
\]
Using valid formulas we can move the existential quantifiers outside the formula.
Size of Generated Formulas
The compositional approach generates a formula polynomial in the size of the program. Indeed, fix the set of variables  . Then:
. Then:
- the size of formula for each basic command is constant
- non-deterministic choice is disjunction
- sequential composition is conjunction (along with renaming that does not affect size–or affects at most
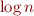 )
)
Moreover, formula generated in such a way looks very much like the program itself, converted to static single assignment form, see