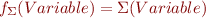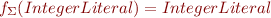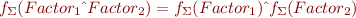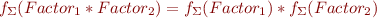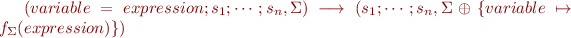Homework 07
Due Wednesday, 24 November, 10:10am. Please hand it in to Hossein before the beginning of the exercise session.
Problem 1
If the following programs type-check according to the rules given in the course, give the corresponding type derivation tree, otherwise give a partial tree that shows where it doesn’t work.
a) Assume the types Pos and Neg are defined as described in the lecture.
def func1( f: Pos => Int): Int = f(5) def func2( f: Int): Neg = -5 val z: Pos = func1(func2)
b) Note that Lists are immutable collections in Scala.
class A class B extends A class C extends B def func1( a: (List[B],List[C]) => List[A]): B def func2( a: List[A], b: List[A]): List[C] val a: Array[A] a(0) = func1(func2)
Problem 2
Recall the TOOTOOL language as defined in the lecture notes. This language supports the following types:
- Int
- Pos <: Int
- Neg <: Int
We slightly change the syntax of the TOOTOOL language so that it allows just multiplication and exponentiation. The new language has the following BNF syntax.
| S | ::= | VarDeclaration* Assignment* |
| VarDeclaration | ::= | var Identifier: Type |
| Assignment | ::= | Identifier = Expression |
| Expression | ::= | Factor ((* | ^) Factor)? |
| Factor | ::= | IntegerLiteral | Variable |
The goal of this exercise is to find a sound type system so that the program never evaluates an expression which has exponentiation by a negative number.
The state of a program at each moment consists of a mapping from its variables to an Int, Pos, or Neg number. Initially all the Int variables have the value 0, the Pos variables have the value 1 and the Neg variables have the value -1.
Given an initial state, we can define the computation of a program. A computation is a series of consecutive configurations of the program. A configuration contains the commands to be executed and the current state. Given a set of assignment commands and an initial state, a computation proceeds following a set of inference rules.
As an example, consider the following piece of code.
var x: Int var y: Pos x = 2 y = 3 x = x ^ y
The initial state as mentioned above is 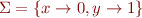 . The computation of the program is as the following.
. The computation of the program is as the following.
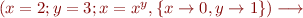
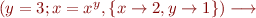
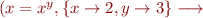
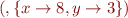
The inference rules are defined using the evaluation function  that evaluates an expression in a give state
that evaluates an expression in a give state  .
.
We have the following inference rule in this version of the TOOTOOL program.
Assume that we have the configuration 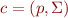 at some point of computation. We say
at some point of computation. We say  is very good if the following two criteria holds.
is very good if the following two criteria holds.
- The program
 is type checked according to the type checking rules.
is type checked according to the type checking rules. - Each variable in
 belongs to the domain determined by its type (if z:Pos, then z is strictly positive).
belongs to the domain determined by its type (if z:Pos, then z is strictly positive).
a) Give the type checking rules that express the properties of multiplication and exponentiation in this setting.
b) Show that if a configuration is very good, after one step of computation according to the inference rule it remains very good in the next configuration.
If your type system of part a does not obey this behavior, you should change it.
c) Use induction to prove that the program never attempts to compute 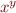 with a negative value
with a negative value  .
.