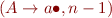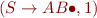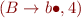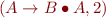Homework 04
Due Wednesday, 3 November, 10:10am. Please hand it in to Hossein before the beginning of the exercise session.
Problem 1
In bottom up parsing replacing the RHS of a rule with its LHS is called reduction. A reductions is called “useless” if it is actually generated during the parsing but it cannot be used in any valid parse tree.
We denote a reduction by a triple (p, A → u, q). We define the fact that a reduction occurs during parsing depending on the parsing technique, as follows.
For CYK: CYK parser, if the non-terminal A belongs to d(p)(q) because of its right-hand side u, that is
- either u is a terminal and is stored at substring from p to q (so q = p+1), or
- u is of the form BC, where B belongs to d(p)(r) and C belongs to d(r+1)(q)
For Earley parser: in Earley parser executes a completion step because of the item 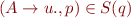
Consider the following grammar.
S -> UT | V "Int" | "Int" T -> V "Int" | "Int" U -> S "=>" V -> T ","
In all of the following questions, consider the input to be “Int , Int ⇒ Int”.
- Construct the CYK parsing table.
- Is the grammar ambiguous for the input?
- Determine the useless reductions in CYK parsing.
- Give the Earley parsing for the same input and grammar.
- Determine the useless reductions in Earley parsing.
- Classify the useless reductions in three categories: both Earley and CYK, only CYK, only Earley.
Problem 2
The Predictor of an Earley parser can be improved by taking into account the look-ahead of the next symbol. As an example if the next symbol of the input is  and
and 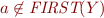 then it will never predict an item of the form
then it will never predict an item of the form  . Describe how this improved Predictor can eliminate some useless reductions in the first problem.
. Describe how this improved Predictor can eliminate some useless reductions in the first problem.
Problem 3
Consider a productive grammar in Chomsky normal form which does not contain  . Assume the input consists of exactly
. Assume the input consists of exactly  tokens, i.e., the lexical analyzer returns
tokens, i.e., the lexical analyzer returns  tokens before hitting the EOF.
tokens before hitting the EOF.
- Assume there are
 productions of form A → BC and
productions of form A → BC and  productions are of form A → a. By considering all the combinations of possible dot positions in the right-hand-side of a production and all different possible values of an item, compute the number of possible items.
productions are of form A → a. By considering all the combinations of possible dot positions in the right-hand-side of a production and all different possible values of an item, compute the number of possible items.
Consider the following grammar.
S -> AB A -> BA A -> a B -> b
Determine which of the following items are possible and which are impossible during the parsing of an input.