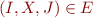Automata for LR Parsing without Lookahead
These automata are used to construct LR(0) and SLR parsers
- same automata, SLR just uses some extra information
We describe their states and transitions
If  was original start symbol, we
was original start symbol, we
- add (D'::=D eof) to grammar
- make
 new start symbol
new start symbol
States: Sets of Items
We will construct states as sets of items
LR(0) item is a dotted production 
 is grammar rule
is grammar rule 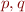 some strings of terminals and non-terminals
some strings of terminals and non-terminals
Note: this is similar to Earley Parser item
- but there is no more initial position!
We use letters I,J to denote sets of LR(0) items
- approximates a set of paths in a syntax tree
- left side of tree corresponds to input seen so far
Example:
Rules in our simple example grammar:
D' ::= E eof E ::= T E ::= E + T T ::= ID
Example state is 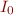 , equal to the following set of items:
, equal to the following set of items:
{ D' ::= .E eof,
E ::= .T,
E ::= .E + T,
T ::= .ID }
Transitions: Closure and Goto Functions
These functions map sets of items to sets of items
Closure is similar to applying prediction in Earley Parser.
If  is a set of states, then closure(I) is least set such that
is a set of states, then closure(I) is least set such that
- I
 closure(I)
closure(I) - if
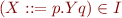 and
and  is a grammar rule, then
is a grammar rule, then 
Example: Take the singleton set
{ D' ::= .E eof }
Then closure of this set is 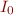 :
:
{ D' ::= .E eof,
E ::= .T,
E ::= .E + T,
T ::= .ID }
where rules are added in this order using the definition.
Goto corresponds to
- scan in Earley Parser when X is a terminal
- completion in Earley Parser when X is a non-terminal

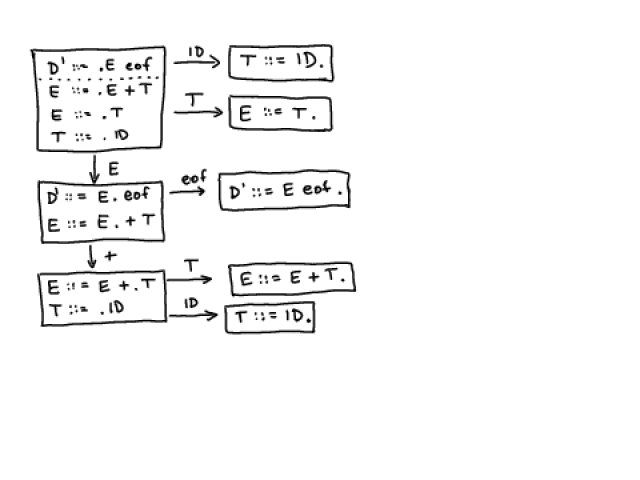
Example: Let us compute goto(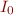 , ID). Because only one element contains .ID, we obtain
, ID). Because only one element contains .ID, we obtain
{ T ::= ID. }
and the closure remains the same because . does not appear before a non-terminal.
I1 = goto(I0, E) = { E ::= E . + T }
I2 = goto(I1, +) = { E ::= E + . T , T ::= . ID }
I3 = goto(I2, T) = { E ::= E + T. }
Constructing Automaton
Initial state 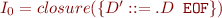
Example: What we denoted 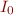 was indeed a correct initial state.
was indeed a correct initial state.
Edges are labeled by grammar terminals and non-terminals
- they are
 function of the Finite state machine
function of the Finite state machine
States and edges are the least sets (T,E) such that

- for each terminal and non-terminal
 and each
and each  , if
, if 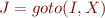 then
then
Examples
The automaton in this example is deterministic
- empty set is dead state
- we do not represent dead state or its edges
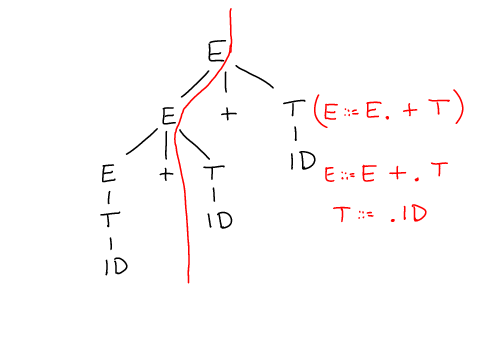
The automaton represents possible sets of slices through syntax trees. The state records, for each non-terminal the way in which it's last ocurrence was unfolded in the tree.
Consider a parse tree for
ID + ID + ID
^
when parser has read only token ID and +, we have the following cut through the tree, and the last expansions of E and T describe the state.