Propositional Logic Semantics
Recall homework01.
Let 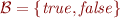 .
.
Interpretation for propositional logic is a function  .
.
We next define evaluation function:
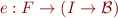
by recursion on formula syntax tree:
This definition follows one in the formula evaluator in homework01.
We denote 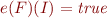 by
by

and denote 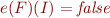 by
by
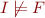
Validity and Satisfiability
Formula is valid iff 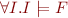 . We write this simply
. We write this simply
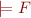
Formula is satisfiable iff 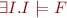
Formula is contradictory iff 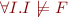
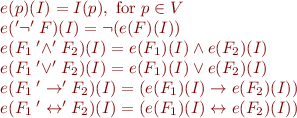
 on left in quotes to emphasize that those are syntactic entities, in contrast to symbols like
on left in quotes to emphasize that those are syntactic entities, in contrast to symbols like  on right-hand side that denote propositional operations given by truth tables (stated in
on right-hand side that denote propositional operations given by truth tables (stated in