Model Checking Finite-State Systems

Suppose we have a finite state system given by an automaton $M$ , compile the specification into an automaton $S$ and check $L(M) \subseteq L(S)$ , that is

$\begin{equation*} L(M) \cap L(S)^c = \emptyset \end{equation*}$

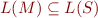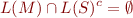
that is, check that the product of automata $M$ and $S$ accepts no strings (each string would be a counterexample).

Some of the operations that we can do on specifications:

for specifications given by formulas: all operations that we can do on formulas ( $\land$ , $\lor$ , $\lnot$ , $\exists$ , $\forall$ , temporal operators, …)
we can also 'ignore' certain parts of the alphabet

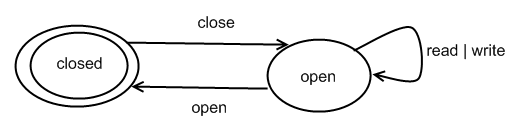
Ignoring Actions Irrelevant for Spec

Suppose we have specification

(open (read+write)* close)*

but our language is as in the Example with Procedures, so it contains many other actions (startLog, endLog, p1Start, p1End, …)

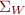Theorem: Let $R$ be a regular language in alphabet $\Sigma$ and $\Sigma_W$ be a disjoint alphabet. Define

$\begin{equation*} R_W = \{ w_0 a_1 w_1 \ldots a_n w_n \mid a_1 \ldots a_n \in R \land w_0,w_1,\ldots,w_n \in \Sigma_W^* \} \end{equation*}$

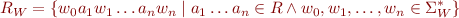
Then 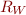$R_W$ is also a regular.

Proof: Consider a finite state machine for $R$ and add self-loops that accept any symbols from $\Sigma_W$ .

Limitations of Finite State Machines

One possibility is to treat procedure calls as gotos.

This corresponds to approximating context-free language of the procedure with a regular one - union of control-flow graphs.

logging can be either on or off in readContent procedure of Example with Procedures
this would result in false warnings