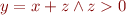Homework 01
Continuing Lab 01
This week, there are two parts to the homework:
- a short (theoretical) pen-and-paper part and
- the first part of the programming project.
Theoretical homework - part 1
Deadline: 4nd March, 2012 (midnight)
Here is an example proof of an inductive invariant, your proof should be of similar formality.
Submission: Please upload the solution as a PDF file through Moodle.
Project - part 1
Deadline: 4nd March, 2012 (midnight) Scala code is to be submitted using git and written answers as a pdf file on moodle.
Setting up your repository
We have set up a version control system around Git, which you can use to share your project code with your partner, but also to submit your project parts. Authentication to this service works by using a SSH key. If you do not already have a private/public key combination for your computer, follow these instructions. Note that you typically generate one key pair per computer that you use.
Once all members of the group have created a key pair, go to http://larasrv05.epfl.ch/sav12 and add you public ssh key in the “Keys” tab of the page (Tequila authentication required.)
Using the Repository From the Command Line
First generate an ssh key pair
- Type
ssh-keygen -t rsa -b 1024. - Type enter to save it in the default location.
- Choose a passphrase, or type enter to ignore it.
- Your public key is now stored in a file (typically, in ~/.ssh/id_rsa.pub). You will need to copy-paste the entire content of this file into our webservice.
Then clone the repository and start using it
- To check out the repository: git clone git@larasrv05.epfl.ch:sav2012-group?? , where you replace ?? with your group number. You can find this URL under the repository tab on the web interface of our system. This will create a copy of the (now empty) repository on your machine.
- Now a SINGLE person in the group should do the following:
- Copy the content of this archive to where she/he cloned the repository.
- Add all the files to the repository using “git add …”
- Finally run “git commit” then “git push origin master”
- All members of the group can now make the files available on their machine by running “git pull” and start working on the project.
- If you want to make the changes you made to the file “some_file” available to your group (i.e. push the file in git terminology), you should first run “git add some_file”, then “git commit”, and finally “git push origin master”, if it is the first time that you push, and otherwise just “git push”.
From Eclipse
If you want to use Eclipse for your programming, see this page for instructions on how to use it with Git and how to generate the SSH key. These instructions were made for a different course. All instructions should apply, but please note the different link to the repository system. You should populate your Eclipse project with the content of this archive
Of course you are free to use any other IDE you like or none at all.
Formulas in Scala
The goal of this first task is to exercise the notions of satisfiability, validity, and equivalence of formulas.
If you set up your repository correctly it should contain the following files:
├── build.xml
├── lib
│ ├── JFlex.jar
│ ├── antlr-3.3-complete.jar
│ ├── java-cup-11a-runtime.jar
│ ├── java-cup-11a.jar
│ └── princess.jar
├── run.sh
├── src
│ └── lazabs
│ ├── Main.scala
│ ├── ast
│ │ └── ASTree.scala
│ ├── prover
│ │ ├── PrincessAPI.scala
│ │ ├── PrincessWrapper.scala
│ │ └── Prover.scala
│ ├── types
│ │ └── Type.scala
│ ├── utils
│ │ └── Manip.scala
│ └── viewer
│ └── ScalaPrinter.scala
└── test
├── example1.scala
├── example2.scala
...
This time you will work with Main.scala, ASTree.scala, and Manip.scala.
Main.scala contains the function that is called when you run your project using the command “./run.sh” at the top level of your project.
Throughout the project we are going to build a program analyzer. Your analyzer will read scala programs, restricted to linear integer arithmetic, and prove properties of these programs, expressed as linear integer arithmetic formulas.
Programs and formulas are represented as trees of objects as defined in ASTree.scala. Such trees are called Abstract Syntax Trees.
Manip.scala contains functions that manipulate abstract syntax trees.
For now the code in Main.scala creates a simple formula and asks the Princess theorem prover to check its satisfiability.
1)Your first task is to find, for each question below, a formula that is satisfiable if and only if the answer to the question is “yes”. We work in the theory of Presburger arithmetic.
- Is the formula
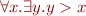 a valid formula?
a valid formula? - Is the formula
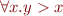 a valid formula?
a valid formula? - Is the formula
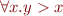 a satisfiable formula?
a satisfiable formula? - Is the formula
 a valid formula?
a valid formula? - Is the formula
 a satisfiable formula?
a satisfiable formula? - Is the formula
 a valid formula?
a valid formula? - Are the following two formulas equivalent?
- Are the following two formulas equivalent?
- Is the formula
 valid? (
valid? ( means modulo)
means modulo)
3)Now modify Main.scala in order to ask Princess the answer to those questions.
2)Finally, explain the answers to each of the questions above.
Tree transformations in Scala
Now that you know how to write formulas in Scala we will learn how to manipulated them. Your task is to modify the file Manip.scala and complete the functions “shortCircuit” and “freeVars”.
The “shortCircuit” function should apply recursively the following rewriting rules to boolean formulas:
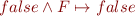 and
and 
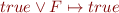 and
and 
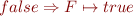
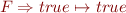
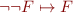
 and
and 
For example, the formula 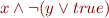 should be rewritten as
should be rewritten as 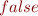 .
.
The “freeVars” function should return the free variables of the given formula. Recall that a variable is free if it is not bound by a quantifier.
For example, the variable x is free in formula 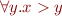 . However variable y is not.
. However variable y is not.
A simple Proof
Consider the code in file test/example11.scala in your repository. Your task is to annotate the file with a loop invariant and extract the verification conditions corresponding to the annotated program.
In other words, find a formula F1 describing the program before the beginning of the loop. The first verification condition should encode the fact that if F1 holds, then the loop invariant holds.
The second verification condition should encode the fact that the loop invariant is preserved by one iteration of the loop.
Finally, the third verification condition should encode the fact if the loop invariant holds and the loop condition does not hold, then the assertion at the end of the program holds.
The validity of these three verification conditions should imply the correctness of the program.
Modify Main.scala to check the validity of your verification conditions.