Homework 04

Finally, things are getting interesting! Or so we hope…

Problem 01: Symbolic Execution

We will keep building on the non-deterministic interpreter from last week. This week you'll add forward symbolic execution to it (similar to Problem 4 in Homework 03 from last year). Here are some points you should pay attention to:

Make sure you don't generate exponentially large formulas (cf. “Merging” on Forward Symbolic Execution).
You should now check assert statements. For this, you will use the SMT solver Z3 (see below for instructions).
You can use the following Scala code to help you generate formulas and check them for satisfiability: Formulas.scala
Your symbolic execution engine should take a loop-free program (which can contain non-deterministic choices and getInts), annotated with assert and assume statements, and check that all assertions hold. That means that you will generate a formula for each assertion and check it with Z3.
Note that the meaning of: x = getInt(e1,e2); is: havoc(x); assume(e1 <= x && x <= e2).

On the following program:

a = 5;
(b = 6; [] b = 7;)
assert(a + b <= 11);
assume(b != 7);
assert(a + b <= 11);

…your symbolic execution engine could say:

assertion "!(11 < (a + b))" does not hold
assertion "!(11 < (a + b))" holds
INVALID

(you can use the pretty-printer we gave you with the parser last time). The last line of your output should always be either

INVALID

if some of the assertions is not guaranteed to hold, or

VALID

if all assertions are guaranteed to hold.

What to Submit

You should submit as part of your solution:

complete source code for your symbolic execution, ready to compile and run
at least 2 interesting test cases in the programming language handled by the symbolic execution engine, accepted by the parser that we supplied in Homework 03

We will collect all examples that you submit and test each submitted symbolic execution engines on each example.

Z3 installation instructions

You will be using the Z3 SMT solver to prove the validity of the verification conditions that you generate. Here is how to install it.

Assuming you are using Linux:

Download Z3 from the following page: http://www.smtexec.org/exec/competitors2008.php (the tarball)
Uncompress the archive. The executable is called run.
Make sure you have an executable called z3 in your path, either by renaming run and moving it, or by creating a symbolic link, eg. in ${HOME}/bin or something similar.
Note that if you already have a version of Z3 for some reason, you should make sure it accepts inputs given not as a file but directly on the standard input (the version we linked to does that).

If you are using Windows, you can download Z3 here: http://research.microsoft.com/projects/z3. You should be able to adapt the Scala code we are giving you, but we don't provide support for that.

You can check that the installation worked by running the following Scala code:

package whilelang
 
object FormulasDemo {
  def main(args: Array[String]): Unit = {
    // You may not want to do the following import if names collide with your other classes       
    import Formulas._
 
    // These implicit conversions can be useful to avoid writing        
    // Var("a") or Const(42) for each variable and numerical constant.  
    implicit def numToConst(n: Int): Const = Const(n)
    implicit def strToVar(s: String): Var = Var(s)
 
    // checks whether 6 * 7 is always equal to 42. In other words,
    // checks that:                                                     
    //                                                                  
    //   !(a = 6 --> 7 * a = 42)                                        
    //                                                                  
    // ...is unsatisfiable.                                             
    val formula = Not(Implies(Equals("a", 6), Equals(Times(7, "a"), 42)))
 
    val result = isSat(formula) match {                                 
      case Some(false) => "unsat"
      case Some(true) => "sat"
      case None => "unknown"
    }
 
    println("The formula:")                                             
    // Prints the formula in SMT format.                                
    println(benchmarkString(formula))
    println("...has the status: " + result + ".")                       
  } 
}

It should say unsat. If an error is reported (for instance, “Z3 complained with: null”), chances are that your Z3 installation was not done correctly.

Note that in your homework, you want to check for validity of formulas, not satisfiability. As you know, this is something you do by using the property that:

“ $\phi$ is satisfiable” $\iff$ “ $\neg \phi$ is valid”

Problem 02

Part a)

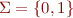Consider regular expressions with variables denoting subsets of $\Sigma^*$ where $\Sigma=\{0,1\}$ . For example,

$\begin{equation*} C\,0 + (A\,1\,B)*B \end{equation*}$

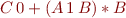
denotes words that either contain a word from the language $C$ followed by symbol 0, or consist of a sequence of words from A1B and a word from B. A word from A1B is simply a word from A, followed by character 1, followed by character 0.

Fix a set $S$ . Define function $W$ that takes such a regular expression and maps them into expressions containing relation variables and relation operators, as follows:

each constant 0 with some relation 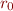$r_0$ and each constant 1 with some relation $r_1$
for each variable $L$ denoting a subset of $\Sigma^*$ (such as A,B,C in example above), it replaces all of its occurrences with a relation variable $r_L$ , denoting relations on $S$
replaces regular set union with relation union $\cup$
replaces concatenation with relation composition $\circ$
replaces language iteration star with transitive closure $*$

Here are some examples of how $W$ works:

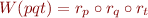
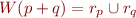
$\begin{equation*} W(pqt) = r_p \circ r_q \circ r_t \end{equation*}$

$\begin{equation*} W(p+q) = r_p \cup r_q \end{equation*}$

$\begin{equation*} W({(p+qp)*}\, p) = (r_p \cup (r_q \circ r_p))^* \circ r_p \end{equation*}$

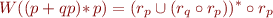
In this part, your task is simply to write a recursive definition of $W$ .

Part b)

Given such definition of $W$ , either prove, or give a counterexample to the following conjecture:

Conjecture: If $R_1$ and $R_2$ are regular expressions containing variables and for all values of variables (subsets of $\Sigma^*$ )

$\begin{equation*} R_1 \subseteq R_2 \end{equation*}$

then for all values of variables (subsets of $S\times S$ )

$\begin{equation*} W(R_1) \subseteq W(R_2) \end{equation*}$

Optional Part c) - Can be Extended into Project

Using results in b) if possible, as well as the meaning of programs as relations, describe informally a procedure that takes two commands $c_1$ and $c_2$ in our simple programming language and attempts to check whether

$\begin{equation*} r_c(c_1) \subseteq r_c(c_2) \end{equation*}$

The procedure should either say

“yes” meaning the subset relation holds, or
“I don't know”, meaning the relation may or may not hold, or
“no”, meaning the relation definitely does not hold

What would your procedure do when $c_1$ is of the form:

if (x < 0)
  if (y < 0)
    s1
  else
    s2
else
  if (y < 0)
    s3
  else
    s4

and $c_2$ is of the form:

if (y < 0)
  if (x < 0)
    s1
  else
    s3
else
  if (x < 0)
    s2
  else
    s4

What if $c_1$ is is as above and $c_2$ is of the form

loop (assume(x<0) [] assume !(x<0) [] 
      assume (y<0) [] assume !(y<0) [] 
      s1 [] s2 [] s3 [] s4)

where loop is the non-deterministic loop construct? Finally, what would it do if $c_1$ is as above and $c_2$ is

loop (s1 [] s2 [] s3 [] s4)

In general, suggest ways to reduce the number of cases when the answer is “I don't know”.