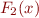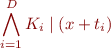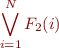Quantifier Elimination for Presburger Arithmetic
(In the language over integers from Definition of Presburger Arithmetic.)
We consider elimination of a quantifier from a conjunction of literals (because QE from Conjunction of Literals Suffices).
Running example:
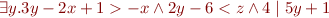
Normalizing Conjunctions of Literals
We first show that we can bring conjunction of literals into a simpler form.
Normal Form of Terms
All terms are built from  , so using standard transformations they can be represented as:
, so using standard transformations they can be represented as:
We call such term a linear term.
Normal Form for Literals
Relation symbols:  ,
,  ,
, 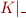 .
.
We obtain a disjunction of conjunctions of literals of the form  and
and 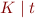 where
where  are of the form
are of the form 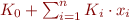
Exposing the Variable to Eliminate
By previous transformations, we are eliminating  from conjunction
from conjunction 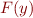 of
of  and
and 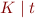 where
where  is a linear term.
is a linear term.
Coefficient next to  :
To eliminate
:
To eliminate  from such conjunction, we wish to ensure that the coefficient next to
from such conjunction, we wish to ensure that the coefficient next to  is one or minus one.
is one or minus one.
Observation:  is equivalent to
is equivalent to  and
and 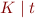 is equivalent to
is equivalent to 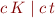 for
for  a positive integer.
a positive integer.
If 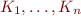 are all coefficients next to
are all coefficients next to  in the formula, let
in the formula, let  be a positive integer such that
be a positive integer such that  for all
for all  ,
, 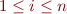 (for example, let
(for example, let  be the least common multiple of
be the least common multiple of 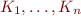 ). Multiply each literal where
). Multiply each literal where  occurs in subterm
occurs in subterm  by constant
by constant 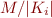 .
.
What is the coefficient next to  in the resulting formula?
in the resulting formula?
We obtain a formula of the form 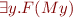 . Letting
. Letting 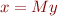 , we conclude the formula is equivalent to
, we conclude the formula is equivalent to 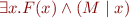 .
.
What is the coefficient next to  in the resulting formula?
in the resulting formula?
Lower and upper bounds:
Consider the coefficient next to  in
in  . If it is
. If it is  , move the term to left side. If it is
, move the term to left side. If it is  , move the remaining terms to the left side. We obtain formula
, move the remaining terms to the left side. We obtain formula 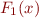 of the form
of the form
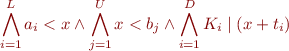
If there are no divisibility constraints (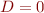 ), what is the formula equivalent to?
), what is the formula equivalent to?
Replacing variable by test terms:
There is a an alternative way to express the above condition by replacing 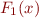 with
with 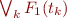 where
where 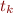 do not contain
do not contain  . This is a common technique in quantifier elimination. Note that if
. This is a common technique in quantifier elimination. Note that if 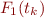 holds then certainly
holds then certainly 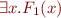 .
.
What are example terms  when
when 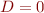 and
and  ? Hint: ensure that at least one of them evaluates to
? Hint: ensure that at least one of them evaluates to  .
.
What if  i.e. we have additional divisibility constraints?
i.e. we have additional divisibility constraints?
Note that if 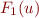 holds then also
holds then also 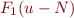 holds.
holds.
That's it for  .
.
What if  ?
?
That's it!
Example
Consider verification condition from Symbolic Execution for Example Integer Program.
How can we prove such verification condition?
The invariant of this code example is : 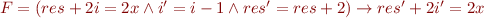
We have to find out if
 is satisfiable.
is satisfiable.
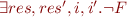
We can eliminate quantifiers with equalities: 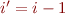 and
and 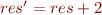
 becomes
becomes  , and
, and 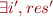 can be removed
can be removed
Finally :

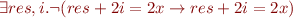
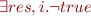
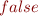
Some Improvements
Avoid transforming to conjunctions of literals: work directly on negation-normal form.
- the technique is similar to what we described for conjunctive normal form
This is the Cooper's algorithm
- Reddy, Loveland: Presburger Arithmetic with Bounded Quantifier Alternation (gives a slight improvement of the original Cooper's algorithm)
- Section 7.2 of the Calculus of Computation Textbook
References
The presentation in thes notes follows Appendix of this report, which also contains further references.
See Section 7.2 of the Calculus of Computation Textbook for a description of more efficient Cooper's algorithm.
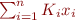
 becomes
becomes 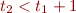
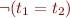 becomes
becomes 
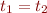 becomes
becomes 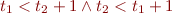
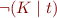 becomes
becomes 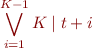
 becomes
becomes 
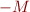
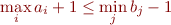
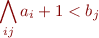
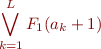
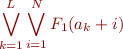
 ?
?