Normal form for loop-free programs
Example:
(if (x < 0) x=x+1 else x=x); (if (y < 0) y=y+x else y=y);
Without loops, after expressing conditionals using [] we obtain
c ::= x=T | assume(F) | c [] c | c ; c
Laws:
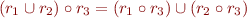
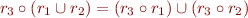
Normal form:
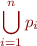
Each 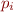 is of form
is of form  for some
for some  , where each
, where each  is assignment or assume. Each
is assignment or assume. Each 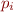 corresponds to one of the finitely paths from beginning to end of the acyclic control-flow graph for loop-free program.
corresponds to one of the finitely paths from beginning to end of the acyclic control-flow graph for loop-free program.
Length of normal form with sequences of if-then-else.
We want to show:
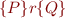
Verifying Each Path Separately
By normal form this is
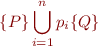
which is equivalent to
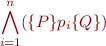
Note: the rule also applies to infinite union of paths (e.g. generated by loops).
Three Approaches to Generate Verification Conditions
Three equivalent formulations of Hoare triple give us three approaches:
- compute meaning of
 as a formula, then check Hoare triple (compositional approach for verification-condition generation)
as a formula, then check Hoare triple (compositional approach for verification-condition generation) - compute
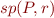 as a formula, then check entailment
as a formula, then check entailment 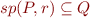 (forward symbolic execution)
(forward symbolic execution) - compute
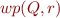 as a formula, then check
as a formula, then check 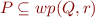 (backward symbolic execution)
(backward symbolic execution)