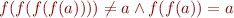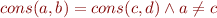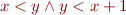Idea of Quantifier-Free Combination
We know of several classes of formulas that we can decide:
- ground formulas interpreted over arbitrary functions and relations (also called uninterpreted function symbols) - congruence closure
- term algebras (interpreted over Herbrand model) - unification
- real linear arithmetic - linear programming such as Simplex
- integer linear arithmetic - integer linear programming (branch and bound, branch and cut), reduction to SAT
We wish to reason about quantifier-free formulas that contain all these different symbols in the same formula.
The idea is to separate a quantifier-free formula into constraints that talk only about individual theories, and solve each constraint separately.
We are checking satisfiability.  is satisfiable iff each disjunct in its disjunctive normal form is satisfiable.
is satisfiable iff each disjunct in its disjunctive normal form is satisfiable.
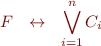
We therefore consider conjunctions of literals  .
.
Consider a conjunction of literals  . If we can group literals into blocks
. If we can group literals into blocks
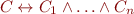
If one of the  is unsatisfiable, then
is unsatisfiable, then  is unsatisfiable.
is unsatisfiable.
The idea is to separate conjuncts into those specific to individual theories, and then solve each  using a specialized decision procedure
using a specialized decision procedure 
An important question is completeness: if each  is satisfiable, is
is satisfiable, is  satisfiable? We will show that, under certain conditions, this holds.
satisfiable? We will show that, under certain conditions, this holds.