This is an old revision of the document!

Forward VCG: Using Strongest Postcondition

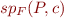If $P$ is a formula on state and $c$ a command, let $sp_F(P,c)$ the formula version of strongest postcondition operator. 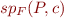$sp_F(P,c)$ is therefore formula $Q$ that describes the set of states that can result from executing $c$ in a state satisfying $P$ .

Thus, we have \[

 sp(\{s.\ f_T(P)(s)\}, r_c(c_1)) = \{ s.\ f_T(sp_F(P,c_1))(s) \}

\] or, less formally, \[

 sp(\{s.\ P\}, r_c(c_1)) = \{ s.\ sp_F(P,c_1) \}

For a predicate $P$ , let $P_s$ be the set of states that satisfies it, \[ P_s = \{s.\ f_T(P)(s) \} \]

Rules for Computing Strongest Postcondition

Assume Statement

Define: \[

 sp_F(P, assume(F)) = P \wedge F

Then \[ \begin{array}{l}

 sp(P_s, assume(F)) \\
 = sp(P_s, \Delta_{F_s}) \\
 = \{s' | \exists s \in P_s.((s,s') \in \Delta_{F_s})\} \\
 = \{s' | \exists s \in P_s.(s=s' \wedge s \in F_s)\} \\ 
 = \{s' | s' \in P_s, s' \in F_s\} = P_s \cap F_s.

\end{array} \]

Havoc Statement

Define: \[

 sp_F(P,\mbox{havoc}(x)) = \exists x_0. P[x:=x_0]

Assignment Statement

Define: \[

 sp_F(P, x = e) = \exists x_0.(P[x:=x_0] \land x=e[x:=x_0])

Indeed: \[ \begin{array}{l}

 sp(P_s, r_c(x = e)) \\
 = \{s'| \exists s.(s \in P_s \wedge (s, s') \in r_c(x=e))\} \\
 = \{s'| \exists s.(s \in P_s \wedge s' = s[x \rightarrow f_T(e)(s)]) \}

\end{array} \]

Sequential Composition

For relations we proved \[

 sp(P_s,r_1 \circ r_2) = sp(sp(P_s,r_1),r_2)

\] Therefore, define \[

 sp_F(P,c_1;c_2) = sp_F(sp_F(P,c_1),c_2)

Nondeterministic Choice (Branches)

We had 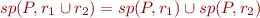$sp(P, r_1 \cup r_2) = sp(P,r_1) \cup sp(P,r_2)$ . Therefore define: \[

 sp_F(P,c_1 [] c_2) = sp_F(P,c_1) \lor sp_F(P,c_2)

Correctness

We show by induction on $c_1$ that for all $P$ : \[

 sp(\{s.\ P\}, r_c(c_1)) = \{ s.\ sp_F(P,c_1) \}

Examples

Example 1. Precondition: 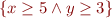$\{x \ge 5 \wedge y \ge 3\}$ . Code:

x = x + y + 10

\[ \begin{array}{l} sp(x \ge 5 \land y \ge 3, x=x+y+10) =

                 \exists x_0.\ x_0 \ge 5 \wedge y \ge 3\ \land\ x = x_0 + y + 10 \\

\leftrightarrow \ y \ge 3 \land x \ge y + 15 \end{array} \]

Example 2 Precondition: $\{x \ge 2 \land y \le 5 \land x \le y \}$ . Code:

havoc(x)

\exists x_0.\ x_0 \ge 2 \land y \le 5 \land x_0 \le y

\] i.e. \[

 \exists x_0.\ 2 \le x_0 \le y \land y \le 5

\] i.e. \[

  2 \le y \land y \le 5

\] If we simply removed conjuncts containing $x$ , we would get just $y \le 5$ .

Size of Generated Formulas

The size of the formula can be exponential because each time we have a nondeterministic choice, we double formula size: \[ \begin{array}{l} sp_F(P, (c_1 [] c_2);(c_3 [] c_4)) =
sp_F(sp_F(P,c_1 [] c_2), c_3 [] c_4) =
sp_F(sp_F(P,c_1) \vee sp_F(P,c_2), c_3 [] c_4) =
sp_F(sp_F(P,c_1) \vee sp_F(P,c_2), c_3) \vee sp_F(sp_F(P,c_1) \vee sp_F(P,c_2), c_4) \end{array} \]

Reducing sp to Relation Composition

The following identity holds for relations (see Sets and Relations): \[

 sp(P,r) = ran(\Delta_P \circ r)

Based on this, we can compute 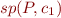$sp(P,c_1)$ in two steps:

compute formula 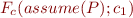$F_c(assume(P);c_1)$ , using Compositional VCG
existentially quantify over initial (non-primed) variables

Indeed, if $F_1$ is a formula denoting relation $r_1$ , that is, \[

  r_1 = \{(\vec x, \vec x\,').\ F_1(\vec x,\vec x\,')

\] then 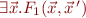$\ \exists \vec x. F_1(\vec x, \vec x\,')$ is formula denoting the range of $r_1$ : \[

 ran(r_1) = \{ \vec x\,'.\ \exists \vec x. F_1(\vec x, \vec x\,') \}

\] Moreover, the resulting approach does not have exponentially large formulas.