This is an old revision of the document!

Exists-Forall Class Definition

Also called Berneys-Schoenfinkel class and Effectively Propositional Logic (EPR).

Notation according to Classical Decision Problem classification: $[\exists^* \forall^*,all,(0)]_{=}$

That means: first-order logic sentences of the form 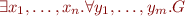$\exists x_1,\ldots,x_n. \forall y_1,\ldots,y_m. G$ where $G$ is quantifier-free formula with equality, with arbitrary relation symbols and constants, but without function symbols.

Summary of restrictions:

only universal quantifiers (the initial existential ones get skolemized in satisfiability checking)
no function symbols

Examples

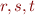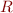For binary relations $r,s,t$ to express $r \circ s \subseteq t$ , we can introduce binary relation symbols $R$ , $S$ , $T$ and write formula \[

  \forall x, y, z. R(x,y) \land S(y,z) \rightarrow T(x,z)

To express 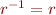$r^{-1} = r$ we would write \[

  \forall x, y. R(x,y) \leftrightarrow R(y,x)

List contains no duplicates: \[

 \forall x,y,z. ListNode(x) \land ListNode(y) \land data(x,z) \land data(y,z) \rightarrow x=y

Relation $r$ is a partial function \[

  \forall x, y_1, y_1. R(x,y_1) \land R(x,y_2) \rightarrow y_1=y_2

We cannot express in this class that 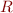$R$ is a total function, or property like 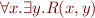$\forall x. \exists y. R(x,y)$ because we need an existential quantifier after a universal one.