Backward VCG: Symbolic Execution using Weakest Preconditions
We again assume for simplicity to have two variables, 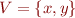 .
.
Rules for Computing Weakest Preconditions
We derive the rules below from the definition of weakest precondition on sets and relations
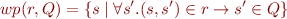
Assume Statement
Suppose we have one variable x, and identify state with that variable. By definition
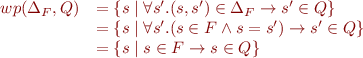
Changing from sets to formulas (and keeping the same name), we obtain the rule for wp on formulas:
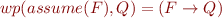
Assignment Statement
Consider the case of two variables. Recall that the relation associated with the assignment x=e is
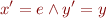
Then we have, for formula  containing
containing  and
and  :
:
![Equation \begin{equation*}
\begin{array}{rl}
wp(r_c(x=e),\{(x,y) \mid Q\}) & = \{(x,y) \mid \forall x'.\forall y'.\ x'=e \land y'=y \rightarrow Q[x:=x',y:=y'] \} \\
& = \{(x,y) \mid Q[x:=e] \}
\end{array}
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/imgc53ca221ddb0742b03336c94d59b6183.png)
From here we obtain:
![Equation \begin{equation*}
wp(x = e, Q) = Q[x:=e]
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img1e7ef52d1c0522cfd022b1b65cceea98.png)
Havoc Statement
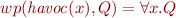
Sequential Composition
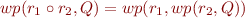
Same for formulas:
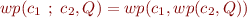
Nondeterministic Choice (Branches)
In terms of sets and relations
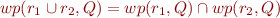
In terms of formulas
![Equation \begin{equation*}
wp(c_1 [] c_2, Q) = wp(c_1,Q) \land wp(c_2,Q)
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img6aa41b99499c50b946cf6e9570b26dcd.png)
Size of Generated Verification Conditions
Because of the rule ![Math $wp(c_1 [] c_2, Q) = wp(c_1,Q) \land wp(c_2,Q)$](/w/lib/exe/fetch.php?media=wiki:latex:/img6e17dd894b712147ab6b5031d4f7b2b8.png) which duplicates
which duplicates  , the size can be exponential.
, the size can be exponential.
More information
- Calculus of Computation Textbook, Chapter 5 (Program Correctness: Mechanics)