Vepar Set Theory
The set theory in Vepar builds ZF set theory through axioms and definitions on top of Vepar HOL.
It defines operations on the  type of Vepar HOL, including the notion of function definition and function application.
type of Vepar HOL, including the notion of function definition and function application.
We believe that the development follows standard set theoretic definitions used by math practitioners, see e.g. Sets and relations.
If we do not say explicitly, we understand that the defined notions and their parameters are all sets, that is, have the type  .
.
Pairs and Cartesian Product
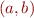 is a shorthand for
is a shorthand for 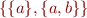 , the standard definition of an ordered pair.
, the standard definition of an ordered pair.
 is
is 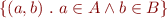
Relation
Def:  is a relation on
is a relation on 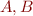 if
if 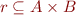 .
.
Total Function
Def: 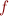 is a total function on
is a total function on 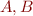 , denoted
, denoted 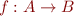 iff
iff 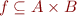 and
and
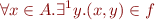
Total Function Application
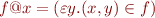
Lemma:
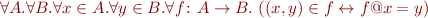
(compare to the definition in Isabelle/ZF)
Set-Theoretic Anonymous Function

means
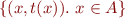
Lemma:
For every expression 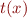
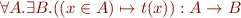
References on set theory
- From http://www.math.unicaen.fr/~dehornoy/surveys.html (in French):
- http://www.math.unicaen.fr/~dehornoy/Surveys/DehornoyChap1.pdf - introduction to sets
- Jech, Thomas (2003), Set Theory: Third Millennium Edition, Springer Monographs in Mathematics, Berlin, New York: Springer-Verlag, ISBN 978-3-540-44085-7