LARA

Homework 2

Due by Monday, 22nd October, 10:15am sharp (right before the class).

Problem 1

Consider the following grammar. 

S -> S S
S -> S '+' S
S -> S '*'
S -> '(' S ')'
S -> 'a' | 'b'

a) How many strings does the grammar generate?

b) Is the language generated by this grammar regular? If it is, give the regular expression, if it is not, explain why.
c) How many distinct parse trees exist for the following string? 

(a*b+a)+(a+b*b)

Now consider the following grammar: 

T -> R
T -> a T c
R ->
R -> R b R

d) How many strings does the second grammar generate?
e) Is the language generated by this grammar regular? If it is, give the regular expression, if it is not, explain why.
f) How many distinct parse trees exist for the following string? 

aaabbbccc

Problem 2

Consider the following grammar over 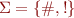$\Sigma = \{\#,!\}$: 

    S -> #A | !# | ! 
    A -> !  | #B | ε
    B -> #B | !

a) Determine how the input string ###! is derived.
b) Find a regular expression that accepts the same language as this grammar.
c) Consider a grammar in which each rule follows one of the following patterns: 

    X -> a
    X -> aY
    X -> Ya
    X -> ε

where $a$ ranges over arbitrary terminals, $X$, $Y$ over arbitrary non-terminals.
Show that every regular language can be represented using a grammar of this form.
Vice versa, can every grammar with these four types of rules be converted into a regular expression?

Problem 3

The following grammar is motivated by type definitions in Scala. 

TypeDefinition  := "type" Identifier "=" Type
Type            := Type ","  Type
Type            := Type "=>" Type
Type            := "Int"  |  "Boolean"

a) By giving at least one input which has two different parse trees prove that the grammar is ambiguous.
b) Given the fact that “=>” has a lower precedence than “,” resolve the ambiguity of the grammar. That is, write a new grammar that determines the same language but is not ambiguous, such that the Type “Int ⇒ Int, Int” is parsed as function from Int to Int,Int.

Problem 4

Let {a, b} be terminals, and {A, B} non-terminals. A production is called linear if it is of the form A → aBb. In other words, if the right hand side can contain only one non-terminal. Show that there are context free languages for which no linear grammar exists.