Homework 03

Due Wednesday, 27 October, 10:10am. Please hand it in to Hossein before the beginning of the exercise session.

Problem 1

A context-free grammar is in Greibach two-standard form if productions are of the following form.

X -> aYZ
X -> aY
X -> a

Prove that for any context-free grammar that does not contain ε there exists an equivalent Greibach two-standard grammar.
Using the Greibach two-standard form prove that the class of context-free languages can be accepted by pushdown_automata.

Problem 2

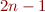Show that if a grammar is in Chomsky normal form then the parse tree for a word of length $n > 0$ has exactly $2n - 1$ interior nodes.

Problem 3

Assume a grammar in Chomsky normal has $n$ non-terminals. Show that if the grammar can generate a word with a derivation having at least $2^n$ steps, then the recognized language should be infinite.

Problem 4

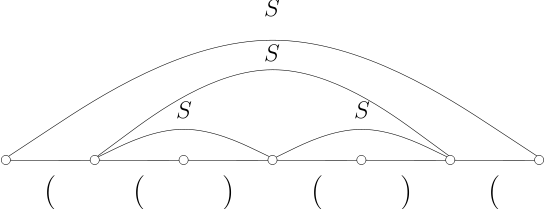
Assume that we want to use the CYK algorithm for the grammars which are not in Chomsky normal form. For example, consider the following grammar for balanced parenthesis.

S -> ( S )
S -> SS
S -> ()

The diagram below shows the parsing for "(()())" using CYK.

Describe why it is not a good idea to use CYK for the arbitrary grammars not in the Chomsky normal form.

Problem 5

A production is called linear if it is of the form A → aBb. In other words, if the right hand side can contain only one non-terminal. Show that there are context free languages for which no linear grammar exists.