Homework 01
Due Wednesday, 13 October, 10:10am. Please Hand it in to Hossein before the beginning of the exercise session.
Problem 1
Given an alphabet  , we define the language double as
, we define the language double as 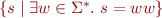 . Prove that double is regular if and only if
. Prove that double is regular if and only if  contains exactly one symbol.
contains exactly one symbol.
Problem 2
Let rtail be a function that returns all the symbols of a string except the last one. For example, rtail(Lexer) = Lexe.
rtail is undefined for an empty string.
If  is a regular expression, then
is a regular expression, then 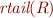 applies the function to all the elements.
For example,
applies the function to all the elements.
For example, 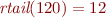 .
.
Prove that 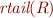 is regular if
is regular if  is not nullable.
is not nullable.
Bonus part: Let  denote the length of the string
denote the length of the string  . Let
. Let  be a regular language. Is the language
be a regular language. Is the language  always regular?
always regular?
Problem 3
Let  be any deterministic finite automaton. Assume that
be any deterministic finite automaton. Assume that  contains exactly
contains exactly  states.
Show that if it accepts at least one string of length
states.
Show that if it accepts at least one string of length  or greater then the accepted language is infinite.
or greater then the accepted language is infinite.
Problem 4
Find a regular expression that generates all the alternating sequences of 0 and 1 with arbitrary length. For example, the alternating sequences of length one are 0 and 1, length two are 01 and 10, length three are 010 and 101. Note that no two adjacent character can be the same in an alternating sequence.
Problem 5
Construct a DFA for the language of nested parenthesis with a maximal nesting depth of 3. For example, ε, ()(), (()(())) and (()())()(), but not (((()))) or (()(()(()))).
Problem 6
a) A lexical analyzer uses the following regular grammar for tokenizing the input string 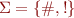 .
.
S -> #A | !# | ! A -> ! | #B | ε B -> #B | !
Determine how the input string '###!' is tokenized.
b) One way to describe the longest match rule is to give priority to the production rules. Give a suitable priority level to the rules of the grammar so that it returns the longest matched tokens.