Subtyping for Functions

To obtain lambda calculus with subtyping, we modify only primitive rules if needed and the application rule for Simple Types for Lambda Calculus.

We modify application rule to allow not only arguments of exact type, but also of subtype:

$\begin{equation*} \frac{\Gamma \vdash e_1 : t_2 \to t_1,\ e_2 : t'_2,\ t'_2 <: t_2} {\Gamma \vdash (e_1\ e_2) : t_1} \end{equation*}$

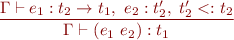
This modification alone allows us to write e.g.

let (f:int->int) = (%x:int. x + 1) in
let (p:pos) = 5 in
  f p

However, it does not allow us to type check code like this:

let (twice:(int -> int)->int) = (% f. f (f 5)) in
let (g:(int->pos)) = (%x:int. 42) in
  twice g

For this purpose, we can define subtyping relation on function types by adding the rule

$\begin{equation*} \frac{t_1 <: t'_1, \ t'_2 <: t_2} {(t_2 \to t_1) <: (t'_2 \to t'_1)} \end{equation*}$

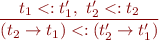
The new application rule then follows as a consequence

We say that

Contravariance of argument may seem surprising at first, but it is the right thing:

compare to modified application rule - $t'_2$ is subtype of $t_2$ , we weakened argument to strengthen type of $e_1$
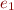
consider interpretation of $t_2 \to t_1$ as a logical implication, and note that in propositional logic the subtyping relation on function types becomes a tautology
ultimate answer is in soundness proof, which can use the meaning of types given by

$\begin{equation*} V_{a \to b} = \{ f\ \mid\ \forall x.\ x \in V_a \rightarrow f(x) \in V_b \} \end{equation*}$

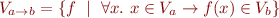
Method Overriding

Rules for function types justify rules for overriding methods