LARA

Homework 04

To be handed out on October 21st, 2009, together with Homework 03.

Consider the following grammar of a simple programming language: 

S :::= E eof
E ::= if (E) E 
E ::= if (E) E else E
E ::= E + E
E ::= (E)
E ::= ID

where the tokens are: 

eof, if, (, ), else, +, id

and nonterminals are S, E.

Part a):

Compute the set follow(E).

Solution:

$follow(E)=\{'+',')','else','eof'\}$

Part b):

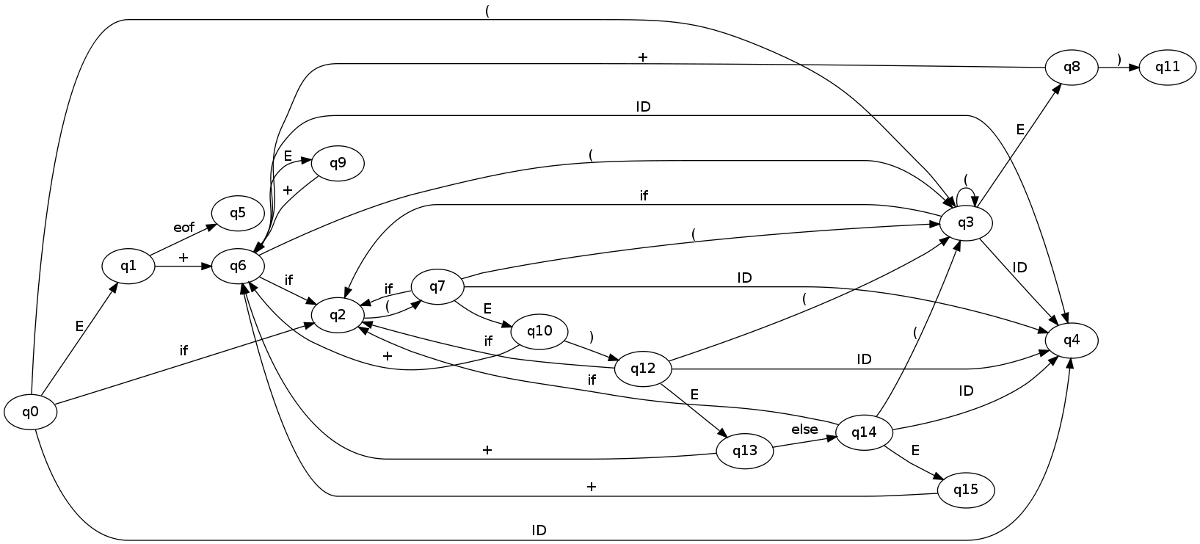
According to Automata for LR Parsing without Lookahead, draw an automaton whose states are sets of LR(0) items and edges are given by the corresponding goto function. Give a name to each state ($q_0, q_1, \ldots, q_n$).

Solution:

The sets of states are:

$q_0 = \{(S\rightarrow .E\,eof),(E\rightarrow .if\,(E)\,E),(E\rightarrow .if\,(E)\,E\,else\,E),(E\rightarrow .E\,+\,E),(E\rightarrow .(E)),$
$(E\rightarrow .ID)\}$
$q_1 = \{(S\rightarrow E\,.eof),(E\rightarrow E\,.+\,E)\}$
$q_2 = \{(E\rightarrow if\,.(E)\,E),(E\rightarrow if\,.(E)\,E\,else\,E)\}$
$q_3 = \{(E\rightarrow (.E),(E\rightarrow .if\,(E)\,E),(E\rightarrow .if\,(E)\,E\,else\,E),(E\rightarrow .E\,+\,E),(E\rightarrow .(E)),$
$(E\rightarrow .ID)\}$
$q_4 = \{(E\rightarrow ID.)\}$

$q_5 = \{(S\rightarrow E\,eof.)\}$
$q_6 = \{(E\rightarrow E\,+\,.E),(E\rightarrow .if\,(E)\,E),(E\rightarrow .if\,(E)\,E\,else\,E),(E\rightarrow .E\,+\,E),(E\rightarrow .(E)),$
$(E\rightarrow .ID)\}$

$q_7 = \{(E\rightarrow if\,(.E)\,E),(E\rightarrow if\,(.E)\,E\,else\,E),(E\rightarrow .if\,(E)\,E),(E\rightarrow .if\,(E)\,E\,else\,E),$
$(E\rightarrow .E\,+\,E),(E\rightarrow .(E)),(E\rightarrow .ID)\}$

$q_8 = \{(E\rightarrow (E.)),(E\rightarrow E\,.+\,E)\}$

$q_9 = \{(E\rightarrow E\,+\,E.),(E\rightarrow E\,.+\,E)\}$

$q_{10} = \{(E\rightarrow if\,(E.)\,E),(E\rightarrow if\,(E.)\,E\,else\,E),(E\rightarrow E\,.+\,E)\}$

$q_{11} = \{(E\rightarrow (E).)\}$

$q_{12} = \{(E\rightarrow if\,(E)\,.E),(E\rightarrow if\,(E)\,.E\,else\,E),(E\rightarrow .if\,(E)\,E),(E\rightarrow .if\,(E)\,E\,else\,E),$
$(E\rightarrow .E\,+\,E),(E\rightarrow .(E)),(E\rightarrow .ID)\}$

$q_{13} = \{(E\rightarrow if\,(E)\,E.),(E\rightarrow if\,(E)\,E\,.else\,E),(E\rightarrow E\,.+\,E)\}$

$q_{14} = \{(E\rightarrow if\,(E)\,E\,else\,.E),(E\rightarrow .if\,(E)\,E),(E\rightarrow .if\,(E)\,E\,else\,E),$
$(E\rightarrow .E\,+\,E),(E\rightarrow .(E)),(E\rightarrow .ID)\}$

$q_{15} = \{(E\rightarrow if\,(E)\,E\,else\,E.),(E\rightarrow E\,.+\,E)\}$

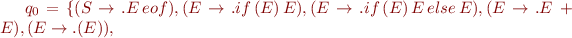
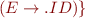
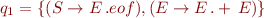
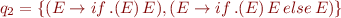
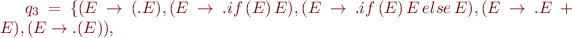
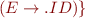
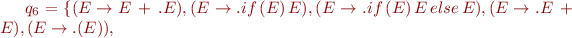
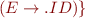
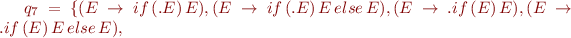
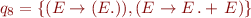
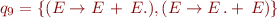
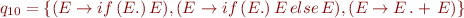
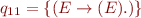
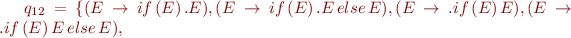
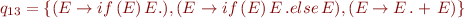
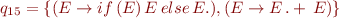
And the corresponding automaton is:

Part c):

Consider the behavior of an SLR Parser for this grammar. List all states $q_i$ that have a conflict where multiple shift or reduce actions are possible. For each such state $q_i$:

  • show an example program that satisfies the grammar and causes the automaton to reach $q_i$ during parsing
  • is it possible to add parentheses (…) to the example so that the parser does not encounter the state $q_i$?
  • recommend a way of resolving the conflicts using associativity rules, if possible

Solution:

  • SR conflicts occur at q9, q15, and q13
  • example input: “x+x+x” gives a conflict at q9, “if (x) (y) else (z)” gives a conflict at q15, and “if (x) (y) else (z) + a” gives a conflict at q15
  • According to the grammar, parentheses can be added with rule $E \rightarrow (E)$. We can remove the conflicts by doing the following: “(x+x)+x” and “(if (x) (y) else (z)) + a”, but we cannot remove the conflict in “if (x) (y) else (z)”.
  • make + associative to the left, then when there is a SR conflict with +, prefer reduce over shift. This solves the conflicts in q9 and q15. For q13, we could have “else” associate to the right and thus prefer shift in case of conflict.